Mikä on Jupyter Notebook?#
Moi! Tämä alusta tässä on Jupyter Notebook. Täällä voit samassa dokumentissa käsitellä tekstiä, koodia, yhtälöitä, kuvia sekä data-aineistoja interaktiivisesti. Näppärää! Näitä dokumentteja kutsutaan notebookeiksi.
Kuten varmaan jo huomasit, tämä alusta toimii sinun internet-selaimessa. Se mahdollistaa oppilaille suunnattujen tehtävien helpon jakamisen ilman kömpelöä välivaihetta, jossa ohjelmistoja pitää ladata ja niiden opettelu vie hirveästi aikaa. Tämän alustan etuja on ehdottomasti helppokäyttöisyys.
Jupyter Notebookia voi käyttää myös lokaalisti, eli asentamalla ohjelman omalle tietokoneelle. Silloinkin tisamalleen samanlainen alusta avautuu selaimeen, mutta voit käyttää sinun koneella olevia tiedostoja suoraan tai tallentaa keskeneräisen tiedoston omalle koneelle. Tämä on kannattavaa silloin, kun haluat luoda omia tehtäviä tai tarkastaa oppilaiden tekemiä vastauksia, jotka sisältävät koodia tai dataa. Esimerkiksi Anaconda-Navigator sisältää Jupyter Notebookin.
Jupyter Notebookien kanssa työskennellessä on hyvä muistaa, että nämä virtuaaliset (ei koske lokaalia työskentelyä) “sessiot” vanhentuvat, jos et ole aktiivinen kymmeneen minuuttiin. Jos uudelleen käynnistys ei onnistu, niin siinä tapauksessa muokatun tiedoston voi vielä tallentaa, jolloin siihen voi palata sitä kautta uudelleen.
Yläpalkista löytyy kaikki tarpeellinen – voit tallentaa tiedoston ja luoda checkpointteja, lisätä tai poistaa uusia soluja, liikutella soluja ylös tai alas sekä ajaa/suorittaa soluja. Alasvetovalikosta voit valita, onko muokkaamasi solu tekstisolu (markdown) vai koodisolu (code).
Jos haluat muokata jotain yksittäistä solua, sen saa editointitilaan tuplaklikkaamalla solua. Muokatun solun voit suorittaa Run-painikkeella tai pikakomentona Control + Enter (Mac: Command + Enter).
# Tältä näyttää koodisolu. Risuaidalla voit kirjoittaa koodisoluun kommentteja tai ohjeita.
# Esimerkin vuoksi tehdään pieni laskutoimitus
a = 1+1 # muuttuja 'a' sisältää nyt laskutoimituksen 1+1
print(a) # tulostetaan muuttuja 'a' näkyviin, jolloin nähdään laskutoimituksen lopputulos.
2
Ylhäällä on koodisolu, joka sisältää pienen laskutoimituksen. Voit suorittaa solun, jolloin sen alapuolelle tulostuu kaikki, mitä koodisolussa käsketään tulostaa. Jos ihan vasemmalla olevissa hakasulkeissa on In [*], niin solun suorittaminen on vielä kesken. Suoritetun koodisolun kohdalla hakasulkeisiin tulee numero, josta näkee, missä järjestyksessä solut on suoritettu. Jos suoritit ylempänä olevan solun kerran, hakasulkeissa pitäisi olla 1, jos suoritat sen saman solun nyt toisen kerran, siihen pitäisi tulla 2.
Tehtävä: Muokkaa tätä tekstisolua – lisää alle lause, jossa kerrot minkälainen sää on tänään.#
Tehtävä: Kokeile lisätä alle uusi koodisolu ja laske jokin mielivaltainen summa muuttujaan b.#
1. Funktiokirjastot#
Pythonia käytettäessä hyödynnetään erilaisia paketteja, joista kukin sisältää oman valikoimansa erilaisia funktioita. Meillä yleisimmin käytössä olevat paketit ovat
numpy, sisältää numeerisen laskennan työkaluja
pandas, sisältää työkaluja datan lukemiseen
matplotlib.pyplot, sisältää kuvaajien piirtotyökaluja
Jokainen haluttu paketti voidaan tuoda erikseen käyttöön import-komennolla.
# Aja tämä solu ensin
import numpy as np # tuodaan numpy-paketti käyttöön ja annetaan sille lyhenne funktioiden kutsumista varten
# Luodaan lista [1 3 6] ja tallennetaan se muuttujaan 'vektori'
vektori = np.array([1,3,6])
print(vektori)
[1 3 6]
Array-funktion avulla voidaan rakentaa taulukoita ja listoja, jolloin sillä voidaan kuvata esimerkiksi vektoreita ja matriiseja. Se sopii myös todella hyvin mittausdatan käsittelyyn.
# Lisätään jokaiseen elementtiin 2.
print(vektori + 2)
[3 5 8]
# Mitä veikkaatte, jos tämän jälkeen printataan pelkkä muuttuja 'vektori'?
print(vektori)
[1 3 6]
vektori = vektori + 2
print(vektori)
[3 5 8]
# Luodaan kaksi listaa ja testataan erilaisia summia.
lista1 = np.array([[2,2],
[1,2]])
lista2 = np.array([[10,11],
[20,21]])
summa = lista1+lista2
print("Listan 1 elementtien summa: ", lista1.sum())
print("Vektorisummmat: ", summa)
Listan 1 elementtien summa: 7
Vektorisummmat: [[12 13]
[21 23]]
Tehtävä: Luo kaksi mielivaltaista vektoria muuttujiin vek1 ja vek2 sekä laske niiden vektorisumma.#
2. Datan lukeminen#
Jupyter Notebookiin voi tuoda datasettejä suoraan avoimien linkkien kautta. Datasettien lukemista varten tarvitaan pandas-pakettia sekä read.csv()-funktiota. CSV (comma-separated values) on tiedostomuoto, jolla voidaan tallentaa yksinkertaista taulukkomuotoista tietoa tekstitiedostoon. Vastaavasti head()-komennolla voidaan kurkistaa datasetin sisälle.
Kokeillaan tätä CERN:n CMS-kokeen avoimella datalla. http://opendata.cern.ch/
import pandas as pd
data = pd.read_csv("http://opendata.cern.ch/record/5209/files/diphoton.csv")
data.head()
| Run | Event | pt1 | eta1 | phi1 | pt2 | eta2 | phi2 | M | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 199319 | 641436592 | 77.2006 | 0.250438 | 0.605505 | 60.1382 | 0.650821 | -1.53900 | 122.797901 |
| 1 | 199699 | 336259924 | 64.1091 | 0.473667 | -0.815133 | 58.6038 | 0.032018 | 2.58568 | 124.586979 |
| 2 | 201602 | 114902683 | 73.7489 | 0.800788 | 0.261020 | 55.9369 | 0.698872 | 3.03502 | 126.462830 |
| 3 | 202087 | 923352992 | 102.9550 | 0.979959 | 0.148624 | 76.6940 | 0.815527 | 1.67359 | 123.622542 |
| 4 | 203894 | 688901524 | 53.4409 | -0.709665 | 1.642300 | 46.4314 | 0.945537 | -2.71670 | 123.203887 |
Jos haluat poimia datasetistä jonkin tietyn muuttujan esimerkiksi kuvaajaa varten, se tapahtuu näin:
# Tietyn sarakkeen poimiminen
invariantti_massa = data['M']
print(invariantti_massa)
# Tietyn rivin poimiminen
rivi = data.loc[1]
print(rivi)
0 122.797901
1 124.586979
2 126.462830
3 123.622542
4 123.203887
5 124.444405
6 124.776915
7 125.704971
8 125.691479
9 123.273271
Name: M, dtype: float64
Run 1.996990e+05
Event 3.362599e+08
pt1 6.410910e+01
eta1 4.736670e-01
phi1 -8.151330e-01
pt2 5.860380e+01
eta2 3.201850e-02
phi2 2.585680e+00
M 1.245870e+02
Name: 1, dtype: float64
Tehtävä: Kokeile avata tässä notebookissa jokin toinen CMS-kokeen datasetti.#
3. Kuvaajat#
Seuraavaksi piirrellään kuvaajia. Sitä varten tarvitaan matplotlip.pyplot -pakettia. Käytetään apuna myös numpy-pakettia, mutta koska se on tuotu meidän käyttöön jo aiemmin, niin sitä ei tarvitse tuoda uudestaan.
import matplotlib.pyplot as plt
# Piirretään kuvaaja sinifunktiosta
x = np.linspace(-np.pi, np.pi)
plt.plot(x, np.sin(x))
plt.xlabel('Kulma [rad]')
plt.ylabel('sin(x)')
plt.title('Kuvaaja 1: Sinifunktio kulman funktiona')
plt.show()
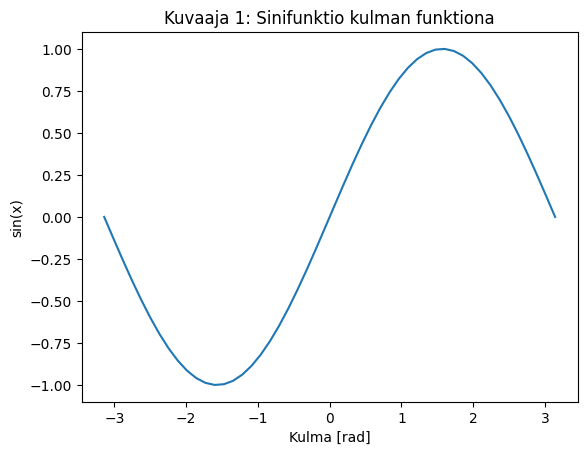
Tehtävä: Piirrä kuvaaja kosinifunktiosta.#
Seuraavaksi yhdistetään: valitaan datasetti ja poimitaan sieltä tiedot haluttua kuvaajaa varten.
kaksi_myonia = pd.read_csv("http://opendata.cern.ch/record/303/files/dimuon.csv")
kaksi_myonia.head()
| Type | Run | Event | E1 | px1 | py1 | pz1 | pt1 | eta1 | phi1 | Q1 | E2 | px2 | py2 | pz2 | pt2 | eta2 | phi2 | Q2 | M | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | GT | 146511 | 25343052 | 7.33390 | 2.060420 | 5.88580 | -3.85836 | 6.23602 | -0.584812 | 1.234060 | -1 | 5.20755 | -1.55016 | -1.819760 | 4.62525 | 2.39050 | 1.414110 | -2.276360 | 1 | 11.82820 |
| 1 | GG | 146511 | 25341481 | 18.46720 | 8.033950 | -3.94072 | -16.15410 | 8.94839 | -1.352990 | -0.456026 | -1 | 10.72950 | 6.29476 | -2.524410 | -8.31349 | 6.78208 | -1.032390 | -0.381397 | 1 | 2.58406 |
| 2 | GG | 146511 | 25390065 | 7.70222 | -0.248771 | 4.08338 | 6.52511 | 4.09095 | 1.246340 | 1.631640 | -1 | 6.90202 | -3.02439 | 3.751290 | 4.94041 | 4.81862 | 0.899132 | 2.249320 | 1 | 3.11929 |
| 3 | GG | 146511 | 25391068 | 6.59462 | 5.246510 | 2.16082 | 3.35900 | 5.67407 | 0.561945 | 0.390686 | 1 | 7.43461 | -5.06069 | 4.408010 | 3.19704 | 6.71127 | 0.459977 | 2.425020 | -1 | 10.51920 |
| 4 | GG | 146511 | 25489877 | 45.77350 | 8.864420 | 1.28931 | -44.88830 | 8.95770 | -2.314620 | 0.144435 | -1 | 9.27485 | -3.64696 | -0.276874 | 8.52260 | 3.65745 | 1.582250 | -3.065820 | 1 | 40.98300 |
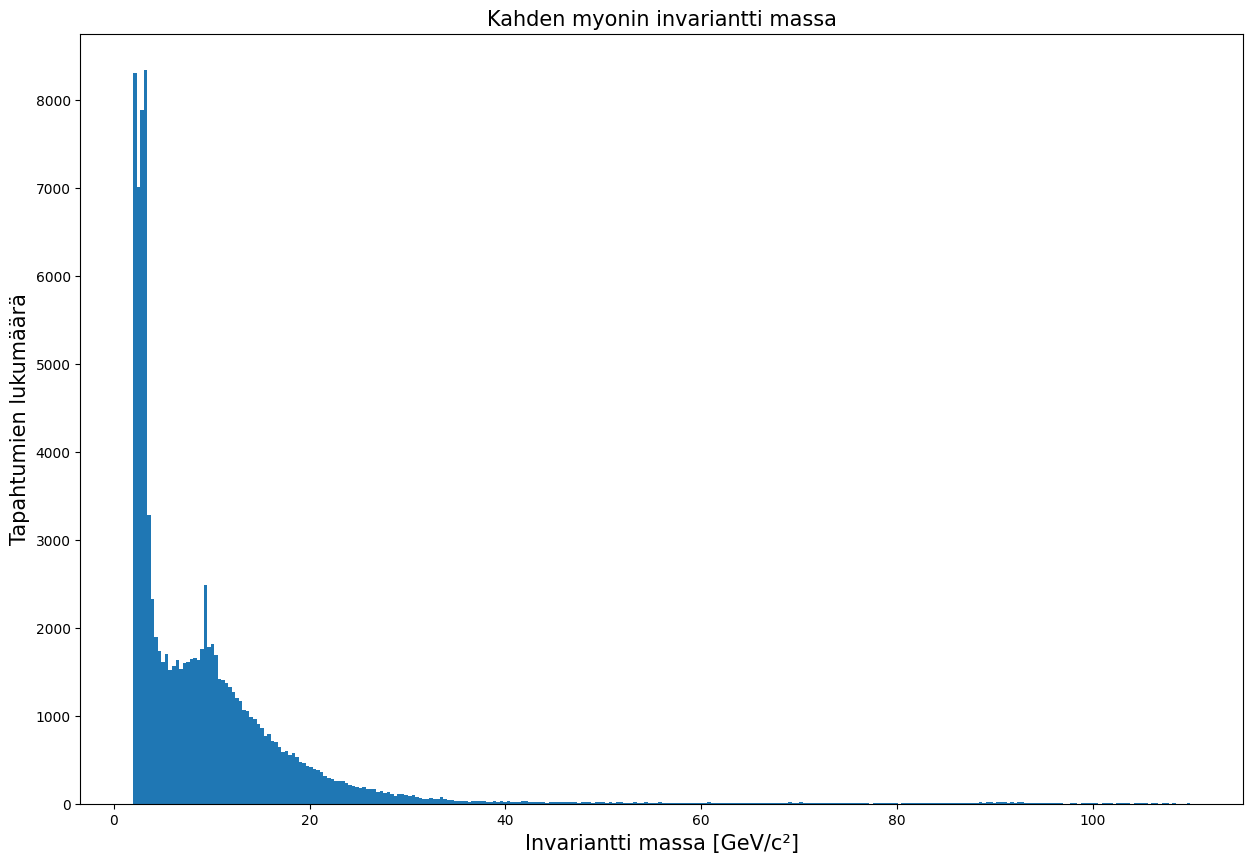
invariantti_massa = kaksi_myonia['M']
fig = plt.figure(figsize=(15, 10))
plt.hist(invariantti_massa , bins=300)
plt.xlabel('Invariantti massa [GeV/c²]', fontsize=15)
plt.ylabel('Tapahtumien lukumäärä', fontsize=15)
plt.title('Kahden myonin invariantti massa', fontsize=15)
plt.show()