Kiihtyvyysmittauksia CMS-koeaseman hississä

Tämä harjoite on esimerkki helposti tehtävästä mittaustyöstä analyyseineen. Alkuperäinen työ toteutettiin vuoden 2024 CERNin opettajakurssille osallistuneitten toimesta.

1. Työkalupaketit

# Ladataan kirjastot
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy import integrate

2. Aineisto

Avataan .csv-tiedosto, joka sisältää puhelimen Phyphox-ohjelmalla https://phyphox.org/ mitattua sensoridataa. Tarkastellaan miltä se näyttää. Data pitää sisällään puhelimen kiihtyvyysanturin mittaukset ajan suhteen, kun CMS-koeaseman hissillä tullaan alhaalta ylös.

df = pd.read_csv('https://raw.githubusercontent.com/opendata-education/Tyopajat/refs/heads/main/materiaali/data/CMS-hissi.csv', delimiter = ";")
df.head()

	Time (s)	Acceleration x (m/s^2)	Acceleration y (m/s^2)	Acceleration z (m/s^2)	Absolute acceleration (m/s^2)
0	0.000305	2.882256	2.801125	7.130572	8.185277
1	0.010345	2.936893	2.764751	7.305109	8.344687
2	0.020386	3.086432	2.800526	7.694449	8.750632
3	0.030428	3.043022	2.689158	8.039182	9.006665
4	0.040470	3.007695	2.600542	8.414153	9.306289

# Acceleration z (m/s^2) on kiihtyvyys puhelimen näyttöön kohtisuorassa suunnassa, eli suunta josta olemme kiinnostuneita.
# Time (s) on kulunut aika.
# Poistetaan ylimääräinen data pudottamalla turhat sarakkeet muuttujasta df.

df.drop(columns = ['Acceleration x (m/s^2)', 'Acceleration y (m/s^2)',"Absolute acceleration (m/s^2)"], inplace = True)

3. Analyysi

# Tarkastellaan datasta alkuun, miltä kiihtyvyys näyttää ajan funktiona.

fig = plt.figure(figsize = (10,3))
plt.plot(df['Time (s)'], df['Acceleration z (m/s^2)'])

plt.xlabel(r'$t\;(\text{s})$')
plt.ylabel(r'$a\;(\text{m/s}^2$)')
plt.title('CMS-hissin kiihtyvyys')
plt.show()

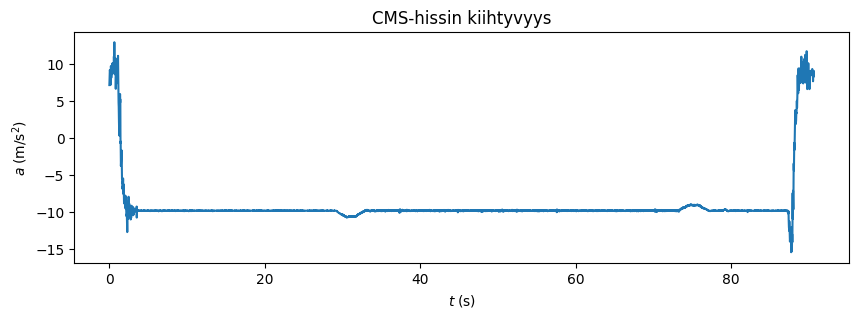
Datasta voidaan päätellä, että puhelin on aluksi ollut näyttö kohden taivasta, minkä jälkeen puhelin on käännetty ylösalaisin ja asetettu hissin lattialle.

# Valitaan datasta tämän takia tarkasteluun väli aikaväli 20-85 s, jolloin
# puhelin on alussa vielä paikoillaan, näyttö kohden hissin lattiaa ja hissi on
# vielä paikoillaan.

df = df.loc[(df['Time (s)'] >= 20) & (df['Time (s)'] <= 85)]

# Tarkastellaan dataa valitulla välillä.

fig = plt.figure(figsize=(10,3))
plt.plot(df['Time (s)'], df['Acceleration z (m/s^2)'])

plt.xlabel(r'$t\;(\text{s})$')
plt.ylabel(r'$a\;(\text{m/s}^2$)')
plt.title('CMS-hissin kiihtyvyys')

plt.show()

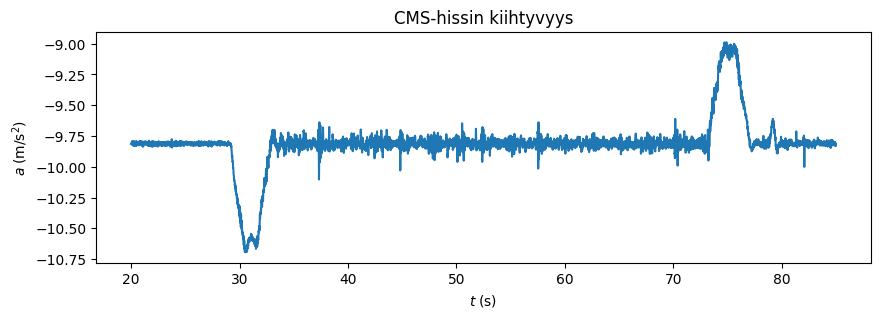
Huomataan, että anturi ilmoittaa kiihtyvyydeksi paikallaan ollessaan noin -9,8 $m/s^2$. Poistetaan tämä esityksestämme määrittämällä keskiarvo kiihtyvyydestä välillä 20-29 s, kun hissi on paikallaan ennen liikkeelle lähtöä.

# Lasketaan keskiarvo tuolta ajalta ja poistetaan se datasta.
# lisäksi käännetään samalla sensorin suunta ottamalla vastaluvut.

a_err = df.loc[df['Time (s)'] <= 29, 'Acceleration z (m/s^2)'].mean()
df.insert(len(df.columns),'Acceleration (m/s^2)',df.loc[:,'Acceleration z (m/s^2)']*(-1)+a_err)
df.head()

	Time (s)	Acceleration z (m/s^2)	Acceleration (m/s^2)
1992	20.002644	-9.813143	0.001534
1993	20.012685	-9.813443	0.001833
1994	20.022727	-9.815838	0.004228
1995	20.032768	-9.818832	0.007222
1996	20.042809	-9.816886	0.005276

# Tarkastellaan dataa korjatulla kiihtyvyyden arvolla.

fig = plt.figure(figsize=(10,3))
plt.plot(df['Time (s)'], df['Acceleration (m/s^2)'])

plt.xlabel(r'$t\;(\text{s})$')
plt.ylabel(r'$a\;(\text{m/s}^2$)')
plt.title('CMS-hissin kiihtyvyys')

plt.show()

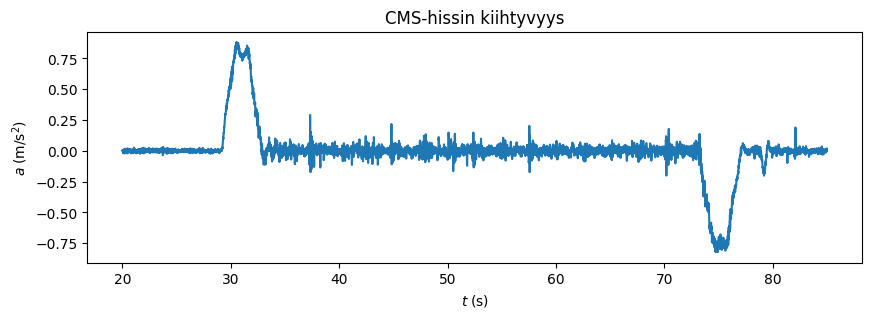
# Määritetään nopeus integroimalla numeerisesti kiihtyvyysdataa ajan suhteen.

velocities = integrate.cumulative_trapezoid(df['Acceleration (m/s^2)'], x=df['Time (s)'], axis=0, initial=0)
df.insert(len(df.columns),'Velocity (m/s)', velocities)

# Määritetään korkeus integroimalla numeerisesti nopeus ajan suhteen.

elevation = integrate.cumulative_trapezoid(df['Velocity (m/s)'], x=df['Time (s)'], axis=0, initial=0)
df.insert(len(df.columns),'Elevation (m)', elevation)

df.head()

	Time (s)	Acceleration z (m/s^2)	Acceleration (m/s^2)	Velocity (m/s)	Elevation (m)
1992	20.002644	-9.813143	0.001534	0.000000	0.000000e+00
1993	20.012685	-9.813443	0.001833	0.000017	8.486443e-08
1994	20.022727	-9.815838	0.004228	0.000047	4.074185e-07
1995	20.032768	-9.818832	0.007222	0.000105	1.171338e-06
1996	20.042809	-9.816886	0.005276	0.000168	2.538876e-06

# Piirretään kuvaaja hissin liikkeestä.

fig, (ax1, ax2, ax3) = plt.subplots(3, sharex=True)
fig = plt.figure(figsize=(10,9))

ax1.set_title('CMS-hissin liike')

ax1.plot(df['Time (s)'], df['Acceleration (m/s^2)'])
ax2.plot(df['Time (s)'], df['Velocity (m/s)'])
ax3.plot(df['Time (s)'], df['Elevation (m)'])

ax1.set_ylabel('$a$ (m/s$^2$)')
ax2.set_ylabel('$v$ (m/s)')
ax3.set_ylabel('$h$ (m)')
ax3.set_xlabel('$t$ (s)')

plt.show()

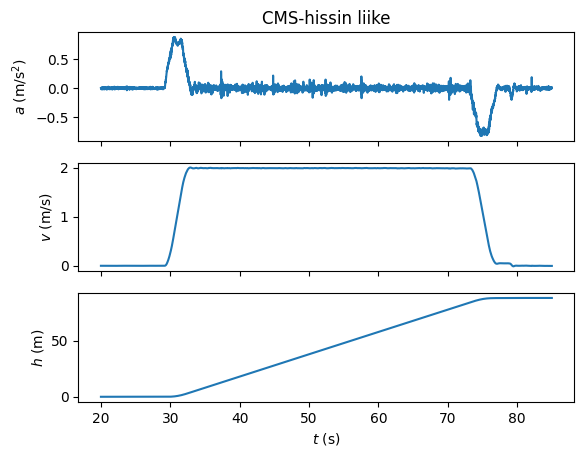
<Figure size 1000x900 with 0 Axes>

# Muutos korkeudessa, joka hissillä noustessa tehtiin.

print(df["Elevation (m)"].max(),"metriä")

87.92253595480473 metriä

4. Johtopäätökset

Tavallisella kännykällä saatiin aika uskottavasti näkyviin kuinka tyypillinen hissi saadaan liikkeelle ja uudelleen lepoon määränpäässään. Voidaanko liikkeen sanoa olleen tasaista vai kiihtyvää matkan aikana?