CMS ja avoin data#
CERN:n CMS-kokeessa törmäytetään protoneita toisiinsa ja tutkitaan, mitä hiukkasia törmäyksessä syntyy. Törmäystapahtumista kertyy valtava määrä dataa, jota on julkaistu myös avoimesti saataville CERN:n avoin data portaalissa. Tässä harjoituksessa tutustutaan siihen, mitä nämä datasetit sisältävät ja mitä niiden avulla voitaisiin selvittää. Tämä tarjoaa oppilaille mainion tilaisuuden kokeilla oikean tieteen metodeja autenttisilla mittaustuloksilla.
1. Datan hakeminen#
Aloitetaan hakemalla data. Data on ladattu CERN:n avoin data portaalista ja tallennettu samaan hakemistoon tämän notebookin kanssa. Tarkastellaan datatiedostoa Dimuon_DoubleMu.csv, joka sisältää dataa törmäystapahtumista, joissa on havaittu kaksi myonia.
# Aloitetaan hakemalla tarvittavat python-paketit import-komennolla
# Voit suorittaa koodisolut Run-painikkeella tai paina CTRL+ENTER.
import pandas as pd
import matplotlib.pyplot as plt
# Luetaan datatiedoston sisältö ja tallennetaan tiedot muuttujaan "kaksi_myonia"
kaksi_myonia = pd.read_csv('http://opendata.cern.ch/record/545/files/Dimuon_DoubleMu.csv')
# Tarkastellaan miltä data näyttää
kaksi_myonia.head()
| Run | Event | type1 | E1 | px1 | py1 | pz1 | pt1 | eta1 | phi1 | ... | type2 | E2 | px2 | py2 | pz2 | pt2 | eta2 | phi2 | Q2 | M | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 165617 | 74601703 | G | 9.6987 | -9.5104 | 0.3662 | 1.8633 | 9.5175 | 0.1945 | 3.1031 | ... | G | 9.7633 | 7.3277 | -1.1524 | 6.3473 | 7.4178 | 0.7756 | -0.1560 | 1 | 17.4922 |
| 1 | 165617 | 75100943 | G | 6.2039 | -4.2666 | 0.4565 | -4.4793 | 4.2910 | -0.9121 | 3.0350 | ... | G | 9.6690 | 7.2740 | -2.8211 | -5.7104 | 7.8019 | -0.6786 | -0.3700 | 1 | 11.5534 |
| 2 | 165617 | 75587682 | G | 19.2892 | -4.2121 | -0.6516 | 18.8121 | 4.2622 | 2.1905 | -2.9881 | ... | G | 9.8244 | 4.3439 | -0.4735 | 8.7985 | 4.3697 | 1.4497 | -0.1086 | 1 | 9.1636 |
| 3 | 165617 | 75660978 | G | 7.0427 | -6.3268 | -0.2685 | 3.0802 | 6.3325 | 0.4690 | -3.0992 | ... | G | 5.5857 | 4.4748 | 0.8489 | -3.2319 | 4.5546 | -0.6605 | 0.1875 | 1 | 12.4774 |
| 4 | 165617 | 75947690 | G | 7.2751 | 0.1030 | -5.5331 | -4.7212 | 5.5340 | -0.7736 | -1.5522 | ... | G | 7.3181 | -0.3988 | 6.9408 | 2.2825 | 6.9523 | 0.3227 | 1.6282 | 1 | 14.3159 |
5 rows × 21 columns
Datatiedostotta näyttäisi olevan paljon tietoa. Jokainen rivi vastaa yhtä törmäystapahtumaa, jossa on havaittu kaksi myonia. Rivillä on aina mittausdataa molemmista havaitusta myonista. Esimerkiksi E tarkoittaa myonin energiaa ja p liikemäärää. Viimeinen sarake M viittaa myoneiden invarianttiin massaan, jota tarkastellaan pian enemmän.
# Katsotaan vielä, kuinka monta riviä dataa tiedostossa on
len(kaksi_myonia)
100000
2. Invariantti massa & histogrammi#
Aiemmasta tutkimuksesta tiedetään, että monet eri hiukkaset voivat hajota kahdeksi myoniksi ja että alkuperäinen hiukkanen voidaan tunnistaa laskemalla myoneiden niin sanottu invariantti massa. CMS-detektorilla voidaan mitata mm. myoneiden energia ja liikemäärä. Kun nämä suureet tiedetään, myoneiden invariantti massa on
$M = \sqrt{(E_1 + E_2)^2 - |\textbf{p}_1 + \textbf{p}_2 | ^2}$.
Mikäli myonit olivat peräisin yhden hiukkasen hajoamisesta, myoneiden invariantti massa vastaa tämän hiukkasen massaa. Jos taas myonit eivät olleet peräisin samasta hiukkasesta, invariantin massan arvo ei merkitse mitään.
Kun protonit törmäävät hiukkaskiihdyttimessä, vapautuu valtava määrä energiaa, joka muuttuu uusiksi hiukkasiksi. Törmäyksessä voisi syntyä esimerkiksi Z-bosoni, joka on kuitenkin niin lyhytikäinen, että se hajoaa nopeasti toisiksi hiukkasiksi, esimerkiksi kahdeksi myoniksi. Nämä myonit havaitaan hiukkasilmaisimessa ja myoneille lasketun invariantin massan avulla pääsemme käsiksi “emohiukkasen” eli tässä tapauksessa Z-bosonin massaan.
Histogrammi on erinomainen työkalu hiukkasfysiikan tutkimuksessa. Tekemällä histogrammin invarianttien massojen arvosta, voimme erottaa merkityksettömistä taustatapahtumista ne tapahtumat, jotka ovat kiinnostavia. Eikun tutkimaan!
# Invariantti massa voitaisiin laskea ylläolevan kaavan avulla.
# Se löytyy kuitenkin valmiiksi laskettuna jo datasetin viimeisestä sarakkeesta "M", joten käytetään sitä.
# Tallennetaan invarianttien massojen sarake omaan muuttujaan
invariantti_massa = kaksi_myonia['M']
# Piirretään histogrammi kahden myonin invarianteista massoista 300 pylväällä
fig = plt.figure(figsize=(15, 10))
plt.hist(invariantti_massa , bins=300)
# Näillä riveillä määritellään otsikko sekä akseleiden tekstit.
plt.xlabel('Invariantti massa [GeV/c²]', fontsize=15)
plt.ylabel('Tapahtumien lukumäärä', fontsize=15)
plt.title('Kahden myonin invariantti massa', fontsize=15)
# Näytetään kuvaaja
plt.show()
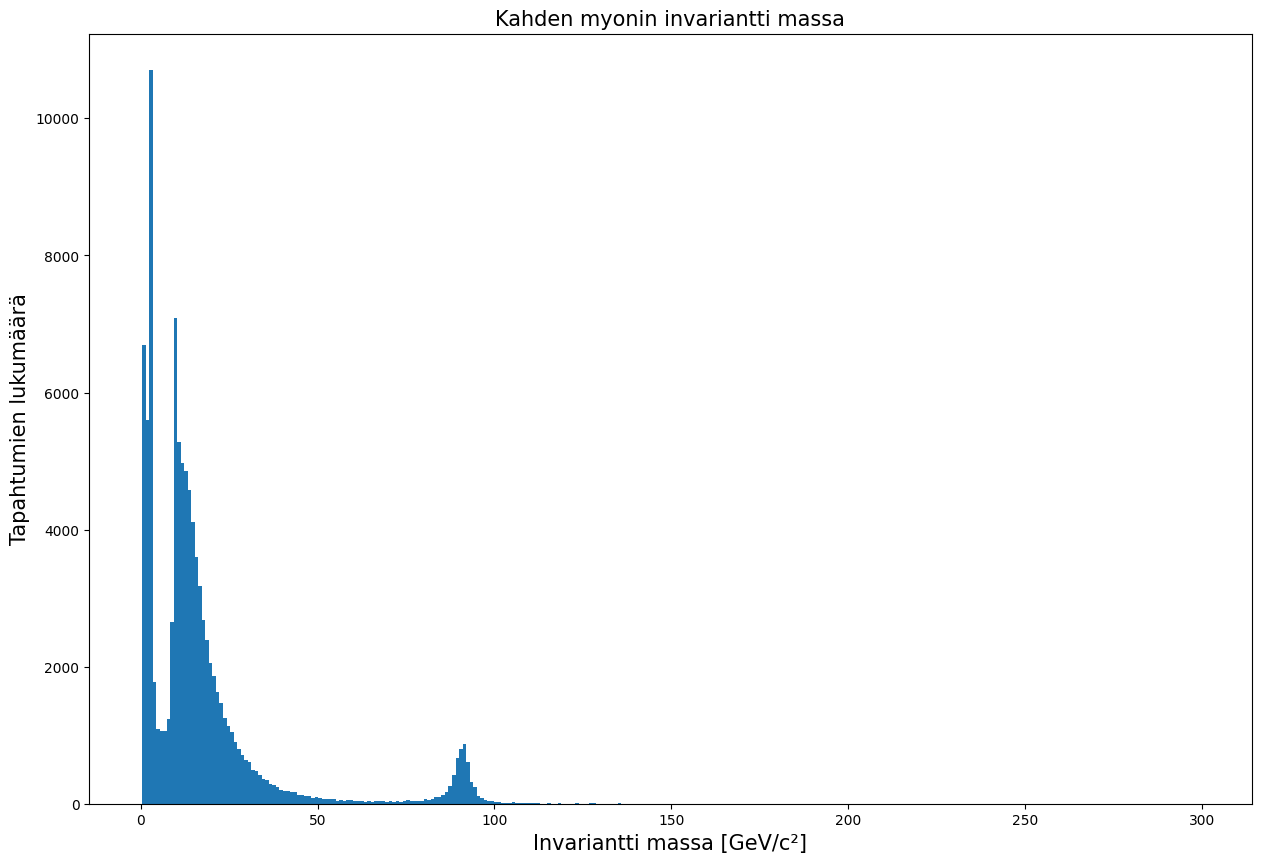
Huomataan, että muutamilla invariantin massan arvoilla histogrammiin syntyy piikki. Nämä piikit vastaavat emohiukkasten massaa, joista kaksi myonia ovat peräisin. Tutkitaan tarkemmin histogrammin väliä 80 GeV - 100 GeV.
# Piirretään histogrammi kahden myonin invarianteista massoista 100 pylväällä välillä 80 GeV - 100 GeV
fig = plt.figure(figsize=(15, 10))
plt.hist(invariantti_massa , bins=100, range=(80,100))
# Näillä riveillä määritellään otsikko sekä akseleiden tekstit.
plt.xlabel('Invariantti massa [GeV/c²]', fontsize=15)
plt.ylabel('Tapahtumien lukumäärä', fontsize=15)
plt.title('Kahden myonin invariantti massa', fontsize=15)
# Näytetään kuvaaja
plt.show()
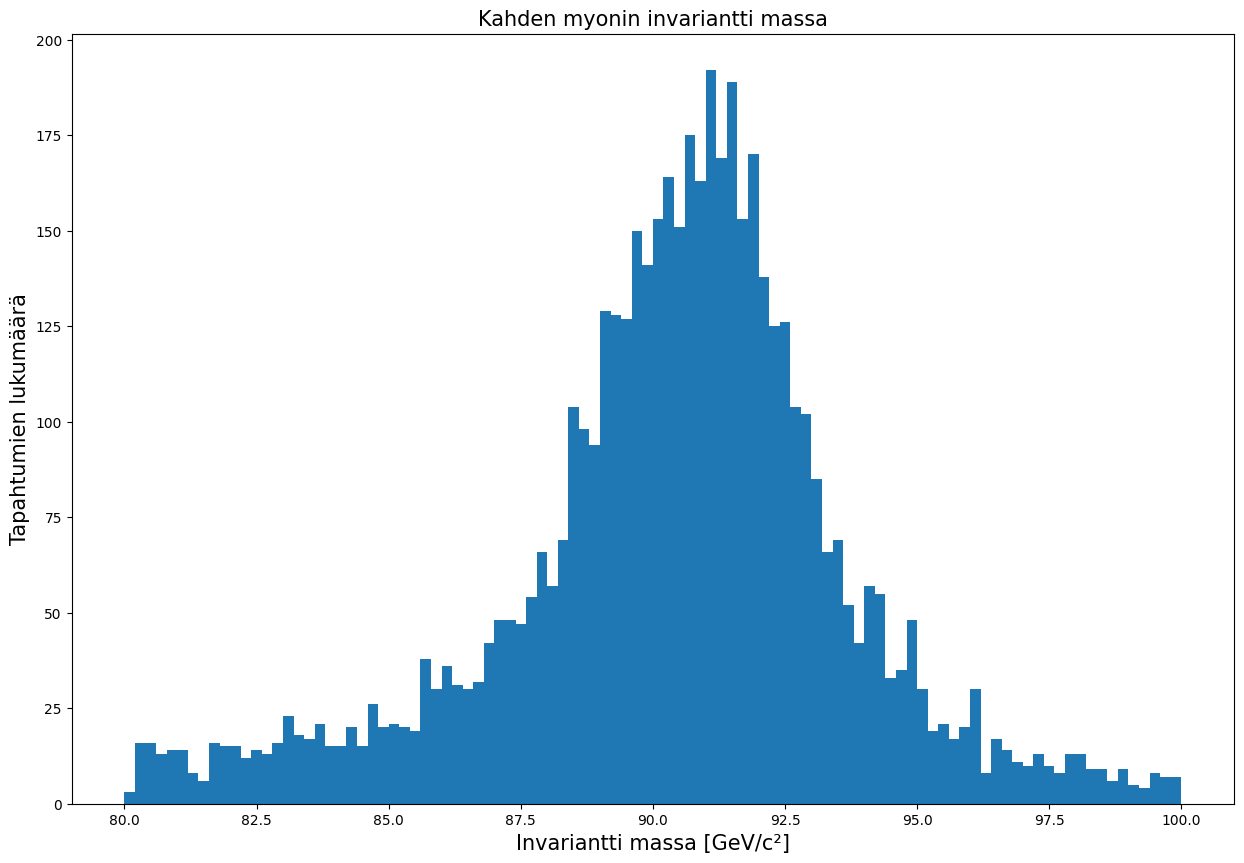
Huomataan, että datasta erottuu selkeä piikki noin 91 GeV kohdalla. Tämä johtuu siitä, taustatapahtumissa syntyvien kahden myonin lisäksi syntyy paljon sellaisia tapahtumia, joissa myonien invariantti massa on lähellä 91 GeV:iä. Tämä tarkoittaa sitä, että myonit ovat peräisin johtain hiukkasesta, jonka massa on 91 GeV. Tämä hiukkanen tunnetaan nimellä Z-bosoni.
Kokeile itse etsiä alkuperäisestä datasta toinen piikki, ja katso löydätkö jonkin toisen hiukkasen! Mikä hiukkanen voisi olla kyseessä?


