Auringonpilkuista

Belgialainen Solar Influences Data Analysis Center julkaisee WDC-SILSO -projektin kautta jatkuvasti päivittyvää aineistoa sivullaan https://www.sidc.be/SILSO/datafiles.

Aurinkoa voi myös tarkastella jatkuvien satelliittikuvien kautta HelioViewerissa: https://gs671-suske.ndc.nasa.gov/.

1. Työkalut

# Aja tämä solu aina ensimmäisenä!

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

2. Aineisto

# Selitteet ja metadata https://www.sidc.be/SILSO/infosndhem

data = pd.read_csv("https://www.sidc.be/SILSO/INFO/sndhemcsv.php", header = None, sep = ";",
                  names = ['Vuosi', 'Kuukausi', 'Päivä', 'Fraktio', '$P_{tot}$', '$P_{poh}$', '$P_{et}$',
                           '$\sigma_{tot}$', '$\sigma_{poh}$', '$\sigma_{et}$', '$N_{tot}$', 
                          '$N_{poh}$', '$N_{et}$', 'Prov'])

<>:5: SyntaxWarning: invalid escape sequence '\s'
<>:5: SyntaxWarning: invalid escape sequence '\s'
<>:5: SyntaxWarning: invalid escape sequence '\s'
<>:5: SyntaxWarning: invalid escape sequence '\s'
<>:5: SyntaxWarning: invalid escape sequence '\s'
<>:5: SyntaxWarning: invalid escape sequence '\s'
/tmp/ipykernel_2160/1511155073.py:5: SyntaxWarning: invalid escape sequence '\s'
  '$\sigma_{tot}$', '$\sigma_{poh}$', '$\sigma_{et}$', '$N_{tot}$',
/tmp/ipykernel_2160/1511155073.py:5: SyntaxWarning: invalid escape sequence '\s'
  '$\sigma_{tot}$', '$\sigma_{poh}$', '$\sigma_{et}$', '$N_{tot}$',
/tmp/ipykernel_2160/1511155073.py:5: SyntaxWarning: invalid escape sequence '\s'
  '$\sigma_{tot}$', '$\sigma_{poh}$', '$\sigma_{et}$', '$N_{tot}$',

data

	Vuosi	Kuukausi	Päivä	Fraktio	$P_{tot}$	$P_{poh}$	$P_{et}$	$\sigma_{tot}$	$\sigma_{poh}$	$\sigma_{et}$	$N_{tot}$	$N_{poh}$	$N_{et}$	Prov
0	1992	1	1	1992.001	186	0	186	14.3	1.0	14.3	19	-1	-1	1
1	1992	1	2	1992.004	190	18	172	8.2	2.6	7.8	21	-1	-1	1
2	1992	1	3	1992.007	234	26	208	18.3	6.1	17.2	21	-1	-1	1
3	1992	1	4	1992.010	243	54	189	14.8	7.0	13.0	20	-1	-1	1
4	1992	1	5	1992.012	242	58	184	13.8	6.8	12.0	18	-1	-1	1
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
12200	2025	5	27	2025.401	104	45	59	9.7	5.9	5.1	25	21	21	0
12201	2025	5	28	2025.404	108	55	53	12.1	8.2	6.5	31	28	28	0
12202	2025	5	29	2025.407	100	56	44	13.2	5.4	8.3	25	22	22	0
12203	2025	5	30	2025.410	117	80	37	13.7	10.5	6.2	34	29	29	0
12204	2025	5	31	2025.412	115	90	25	12.8	11.2	5.3	30	23	23	0

12205 rows × 14 columns

3. Analyysi

# Saraketsikot näkyvät datan haussa, mutta eritellään ne vielä tähän.
data.columns

Index(['Vuosi', 'Kuukausi', 'Päivä', 'Fraktio', '$P_{tot}$', '$P_{poh}$',
       '$P_{et}$', '$\sigma_{tot}$', '$\sigma_{poh}$', '$\sigma_{et}$',
       '$N_{tot}$', '$N_{poh}$', '$N_{et}$', 'Prov'],
      dtype='object')

# Valitse haluamasi sarake y-akseliksi

ehto = "$P_{tot}$"

# Asetetaan kuvaajan suhteet
plt.figure(figsize = (20,5))

# Piirretään käyrät
plt.plot(data["Fraktio"], data[ehto], c = "y", alpha = 0.5)
plt.scatter(data["Fraktio"], data[ehto], c = "firebrick")

# Laitetaan selitteet paikoilleen
plt.title(f"Auringonpilkkujen päivittäinen määrä, {ehto} \n", fontsize = 20)
plt.ylabel("Määrä (n)", fontsize = 15)
plt.xlabel("Aika (fraktio)", fontsize = 15)

plt.show()

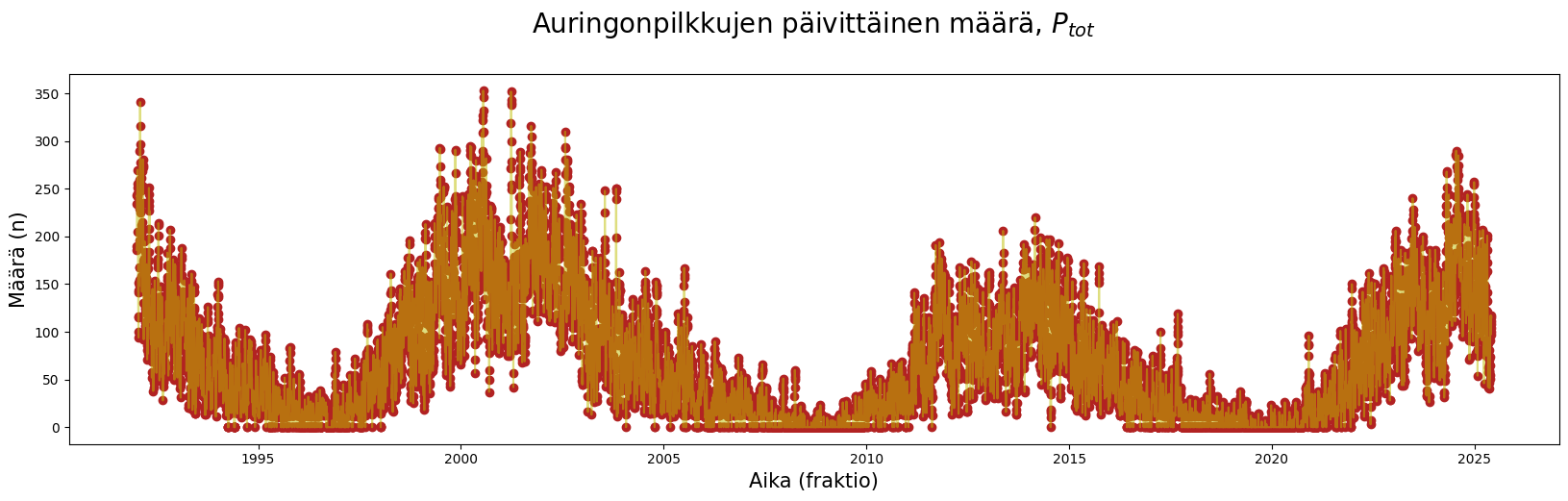
Eritellääs vähän eri auringonpuoliskojen välillä.

# Valitse haluamasi sarake y-akseliksi

ehto1 = "$P_{poh}$"
ehto2 = "$P_{et}$"

# Asetetaan kuvaajan suhteet
plt.figure(figsize = (20,5))

# Piirretään käyrät
plt.plot(data["Fraktio"], data[ehto1], c = "y", alpha = 0.5)
plt.scatter(data["Fraktio"], data[ehto1], c = "firebrick", label = ehto1)

plt.plot(data["Fraktio"], data[ehto2], c = "grey", alpha = 0.5)
plt.scatter(data["Fraktio"], data[ehto2], c = "slateblue", label = ehto2)

# Laitetaan selitteet paikoilleen
plt.title(f"Auringonpilkkujen päivittäinen määrä, {ehto1} ja {ehto2} \n", fontsize = 20)
plt.ylabel("Määrä (n)", fontsize = 15)
plt.xlabel("Aika (fraktio)", fontsize = 15)

plt.legend(fontsize = 15)
plt.show()

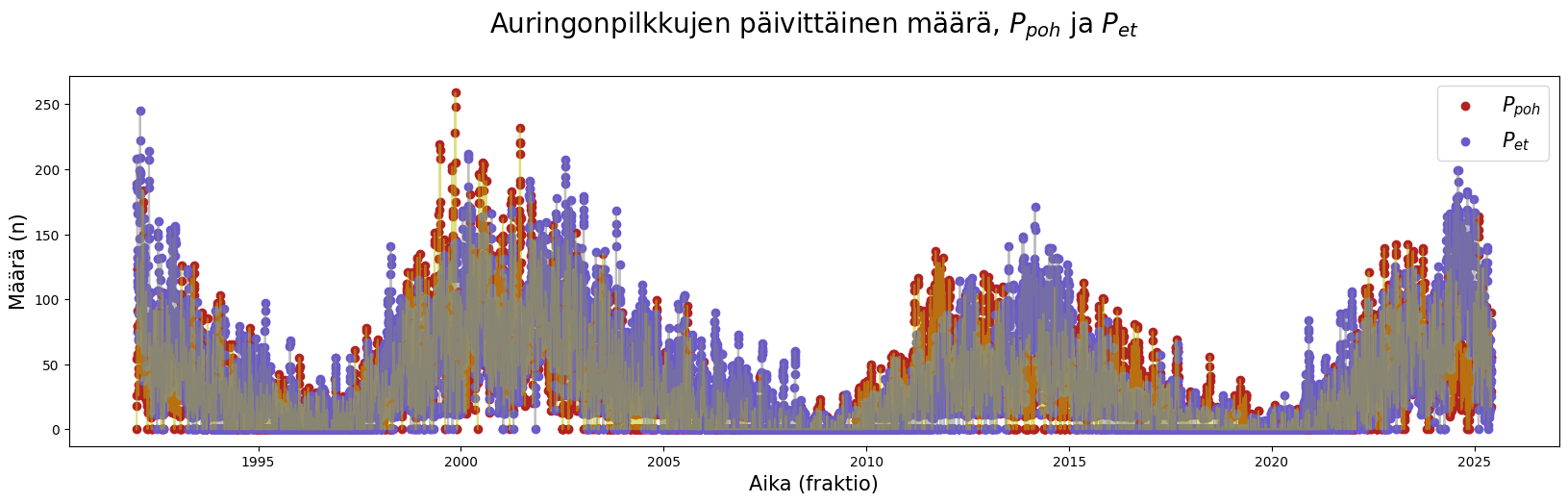
Näyttää vähän ahtaalta. Päivittäisten tietojen tuhansien pisteiden sijasta meidän olisi ehkä hyödyllistä jaotella materiaalia hieman ymmärrettävämpiin osasiin. Näitä voisivat olla esimerkiksi yhden vuoden havainnot, vuosien keskiarvot, kuukausittaiset arvot jne.

# Mittapisteitä on niin paljon, että eritellään aineistoa hieman. Otetaan yksi vuosi tarkasteluun.

vuosi = 1998
valinta = data.query("Vuosi == @vuosi")

plt.figure(figsize = (20,10))
plt.scatter(valinta["Fraktio"], valinta["$P_{tot}$"])

maksimi = valinta["$P_{tot}$"].max()
minimi = valinta["$P_{tot}$"].min()

tieto = f"Vuoden korkein päiväarvo oli {maksimi} kappaletta ja matalin {minimi} kappaletta."

plt.title(f"Auringonpilkut vuonna {vuosi}. \n {tieto}", fontsize = 20)
plt.ylabel("$P_{tot}$", fontsize = 15)
plt.xlabel("\n Aika (fraktio)", fontsize = 15)
plt.show()

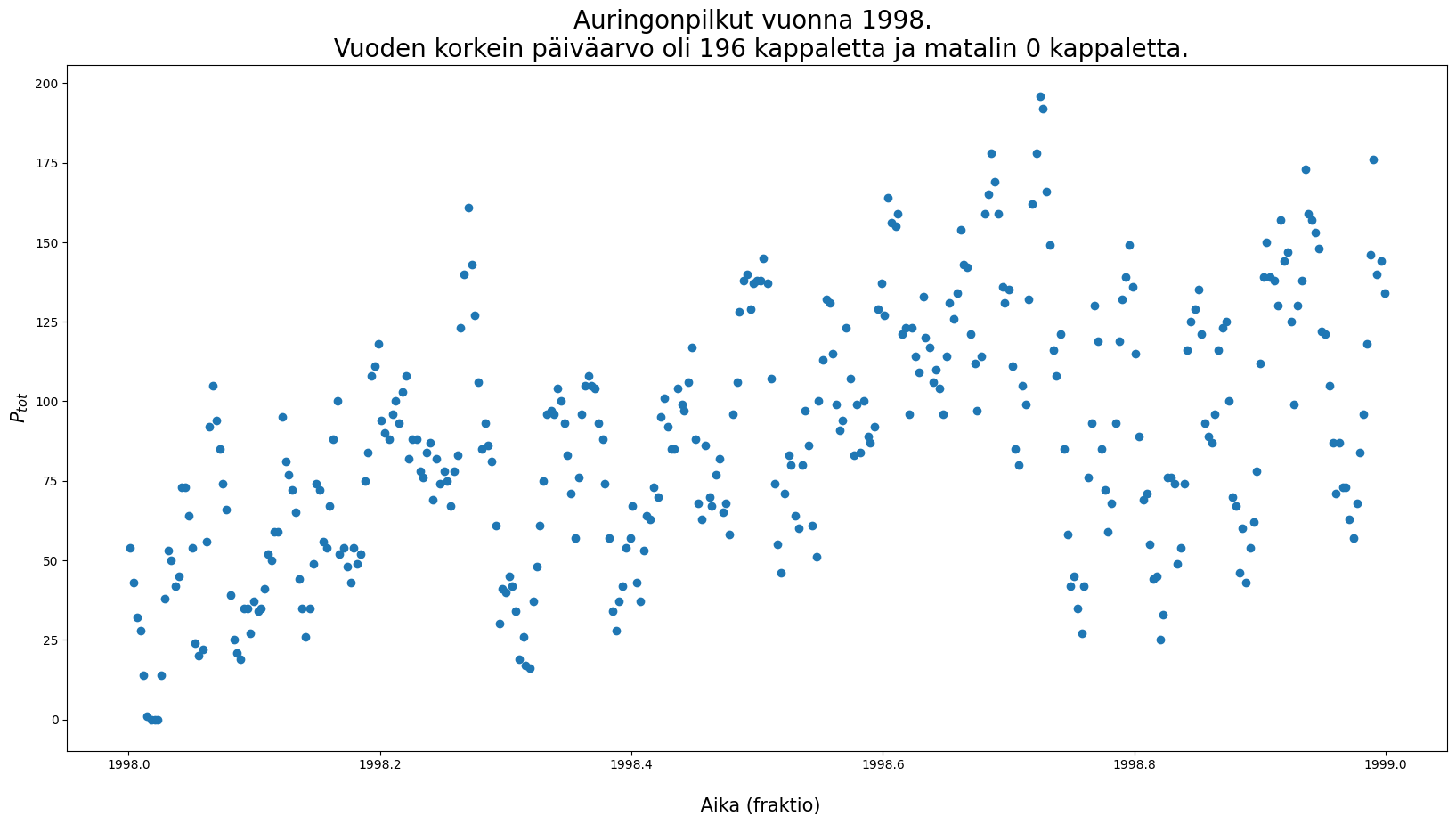
# Lisätään äskeiseen vielä sovite, jos sieltä vaikka löytyisi jonkinlainen kuvio.

vuosi = 1998
valinta = data.query("Vuosi == @vuosi")
vaaka = valinta["Fraktio"].copy()

plt.figure(figsize = (20,10))

plt.plot(vaaka, valinta["$P_{tot}$"], c = "y", alpha = 0.5)
plt.scatter(vaaka, valinta["$P_{tot}$"], c = "firebrick", label = "$P_{tot}$")

# Trendi.
x = np.arange(len(vaaka))
y = valinta["$P_{tot}$"].copy()

# Tästä lukua vaihtamalla voi muuttaa sovitetun yhtälön astetta.
z = np.polyfit(x, y, 3)
p = np.poly1d(z)
plt.plot(vaaka, p(x), c = "black", linestyle = "dashed", label = "trendiviiva", alpha = 0.7)

maksimi = valinta["$P_{tot}$"].max()
minimi = valinta["$P_{tot}$"].min()

tieto = f"Vuoden korkein päiväarvo oli {maksimi} kappaletta ja matalin {minimi} kappaletta."

plt.title(f"Auringonpilkut vuonna {vuosi}. \n {tieto}", fontsize = 20)
plt.ylabel("$P_{tot}$", fontsize = 15)
plt.xlabel("\n Aika (fraktio)", fontsize = 15)
plt.legend(fontsize = 15)
plt.show()

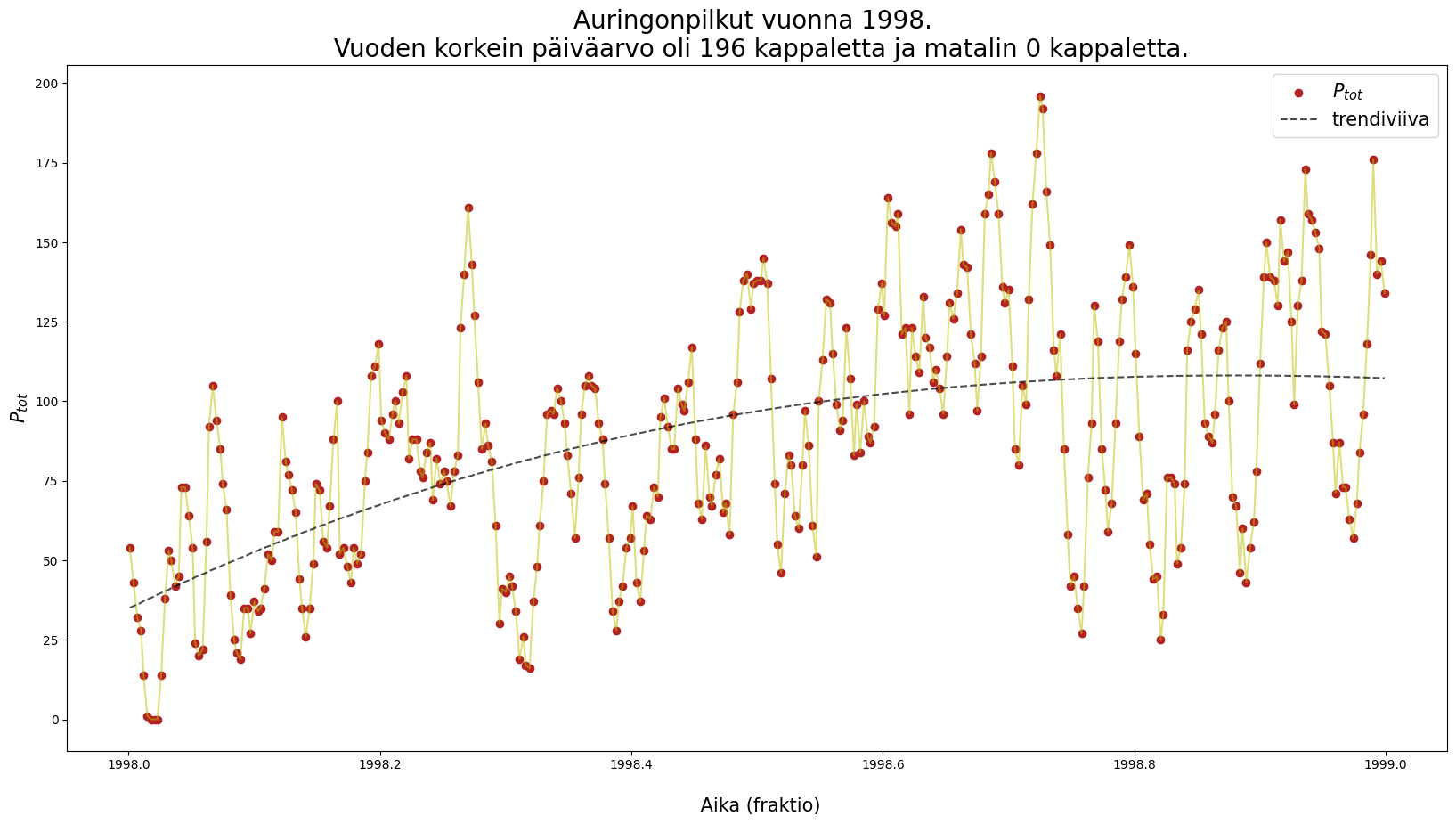
# Saisitko samanlaisen leikkauksen esittämään valitun vuoden aineiston eri auringonpuoliskojen mukaan?
# Koodaile tänne.

Mites vuosikeskiarvot?

ehto = "Vuosi"
suure = "$P_{tot}$"

KAV = data.groupby([ehto]).mean(numeric_only = True)
vaaka = data[ehto].unique()

plt.figure(figsize = (10, 5))

plt.plot(vaaka, KAV[suure], c = "y", alpha = 0.5)
plt.scatter(vaaka, KAV[suure], c = "firebrick")

plt.title(f"{suure}, vuosikeskiarvo", fontsize = 20)
plt.ylabel("Määrä (n)", fontsize = 15)
plt.xlabel("\n Aika (fraktio)", fontsize = 15)
plt.show()

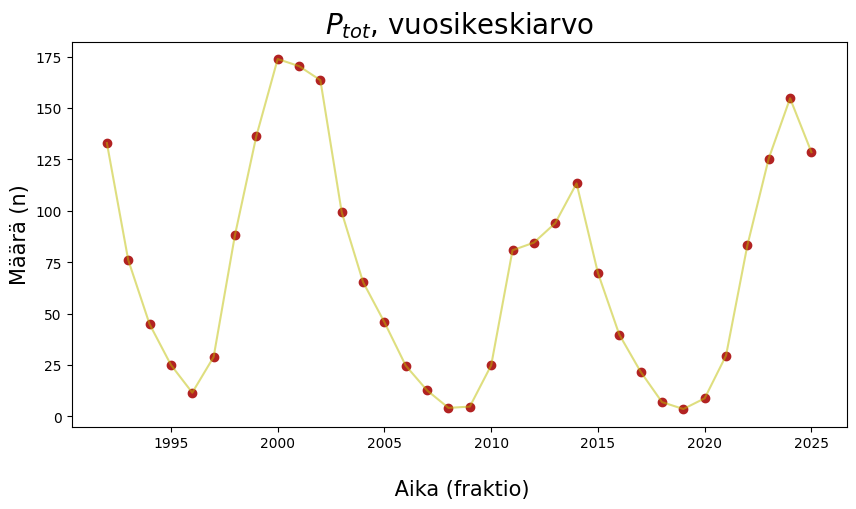
Millaisella syklillä tilanne muuttuu?

Onko auringonpuoliskoilla eroja?

Minä vuonna on havaittu korkein yksittäinen havainto? Mikä päivä oli kyseessä?

Aineistossa on mukana myös keskihajonta. Jos tekisit kuvaajan, jossa on mukana pidemmän ajan keskiarvo ja sitä ympäröivät hajontarajat, miten usein havainnot pomppivat sen ylitse?

# Koodaile tänne tai lisäile soluja oman tarpeesi mukaan!