CMS ja avoin data

CERNissä tuotetaan valtavat määrät dataa jatkuvasti. Compact Muon Solenoid (eli CMS) -koe on julkaissut omaansa avoimeen jakoon hirvittäviä määriä vuodesta 2014 lähtien ja seuraavan vuosikymmenen mittaan laitetaan loputkin. Vuoden 2023 aikana lähes kaikki ensimmäisten LHC-ajojen aikaiset havainnot löytyvät CERNin avoimen datan portaalista (https://opendata.cern.ch/).

Tutustutaan tässä harjoitteessa tapoihin, joilla voidaan tarkastella mitä näistä mittauksista voitaisiin selvittää. Tämä tarjoaa opiskelijoille mainion tilaisuuden puuhastella autenttisen huippututkimuksen aineistojen parissa.

1. Käytetty data

# Olen koodisolu! Risuaidalla merkattu rivi on kommentti, joka tekee koodista ihmiselle luettavampaa.
# Aja tämä solu ensin, jotta python tietää mitä sillä ollaan tekemässä (eli haetaan sopivat paketit).

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Avataan muutaman törmäytyksen tapahtumat.

kaksoismyonit = pd.read_csv('https://raw.githubusercontent.com/cms-opendata-education/cms-jupyter-materials-finnish/master/Data/Dimuon_DoubleMu.csv')
jpsi = pd.read_csv('https://raw.githubusercontent.com/cms-opendata-education/cms-jupyter-materials-finnish/master/Data/Jpsimumu_Run2011A.csv')

# Tarkastellaan miltä data näyttää. Voit kokeilla myös jpsi.head(), laittaa sulkuihin numeron jne.

kaksoismyonit.head()

	Run	Event	type1	E1	px1	py1	pz1	pt1	eta1	phi1	...	type2	E2	px2	py2	pz2	pt2	eta2	phi2	Q2	M
0	165617	74601703	G	9.6987	-9.5104	0.3662	1.8633	9.5175	0.1945	3.1031	...	G	9.7633	7.3277	-1.1524	6.3473	7.4178	0.7756	-0.1560	1	17.4922
1	165617	75100943	G	6.2039	-4.2666	0.4565	-4.4793	4.2910	-0.9121	3.0350	...	G	9.6690	7.2740	-2.8211	-5.7104	7.8019	-0.6786	-0.3700	1	11.5534
2	165617	75587682	G	19.2892	-4.2121	-0.6516	18.8121	4.2622	2.1905	-2.9881	...	G	9.8244	4.3439	-0.4735	8.7985	4.3697	1.4497	-0.1086	1	9.1636
3	165617	75660978	G	7.0427	-6.3268	-0.2685	3.0802	6.3325	0.4690	-3.0992	...	G	5.5857	4.4748	0.8489	-3.2319	4.5546	-0.6605	0.1875	1	12.4774
4	165617	75947690	G	7.2751	0.1030	-5.5331	-4.7212	5.5340	-0.7736	-1.5522	...	G	7.3181	-0.3988	6.9408	2.2825	6.9523	0.3227	1.6282	1	14.3159

5 rows × 21 columns

# Katsotaan paljonko tapahtumia näissä seteissä on.

print (len(kaksoismyonit))
print (len(jpsi))

100000
31892

2. Invariantti massa

Invariantti massa on matemaattinen suure, jonka avulla voidaan selvittää millaisen hiukkasen hajoamisesta törmäyksessä havaitut hiukkaset liikemäärineen ja energioineen syntyivät. Sillä on suuri merkitys hiukkastutkimuksessa, jossa monesti etsitään tietyille massoille ennustettujen hiukkasten piikkejä havainnoista.

Histogrammi on voimakas työkalu tällaiseen tarkoitukseen.

# Suoritetaan histogrammin piirtäminen:

fig = plt.figure(figsize = (15, 10))
plt.hist(kaksoismyonit.M, bins = 100)

# Näillä riveillä ainoastaan määritellään otsikko sekä akseleiden tekstit.

plt.xlabel('Invariantti massa [GeV/c²]', fontsize = 15)
plt.ylabel('Tapahtumien lukumäärä', fontsize = 15)
plt.title('Kahden myonin invariantin massan histogrammi \n', fontsize = 15) # \n luo uuden rivin otsikon muotoilua varten

# Tehdään kuvaaja näkyväksi.

plt.show()

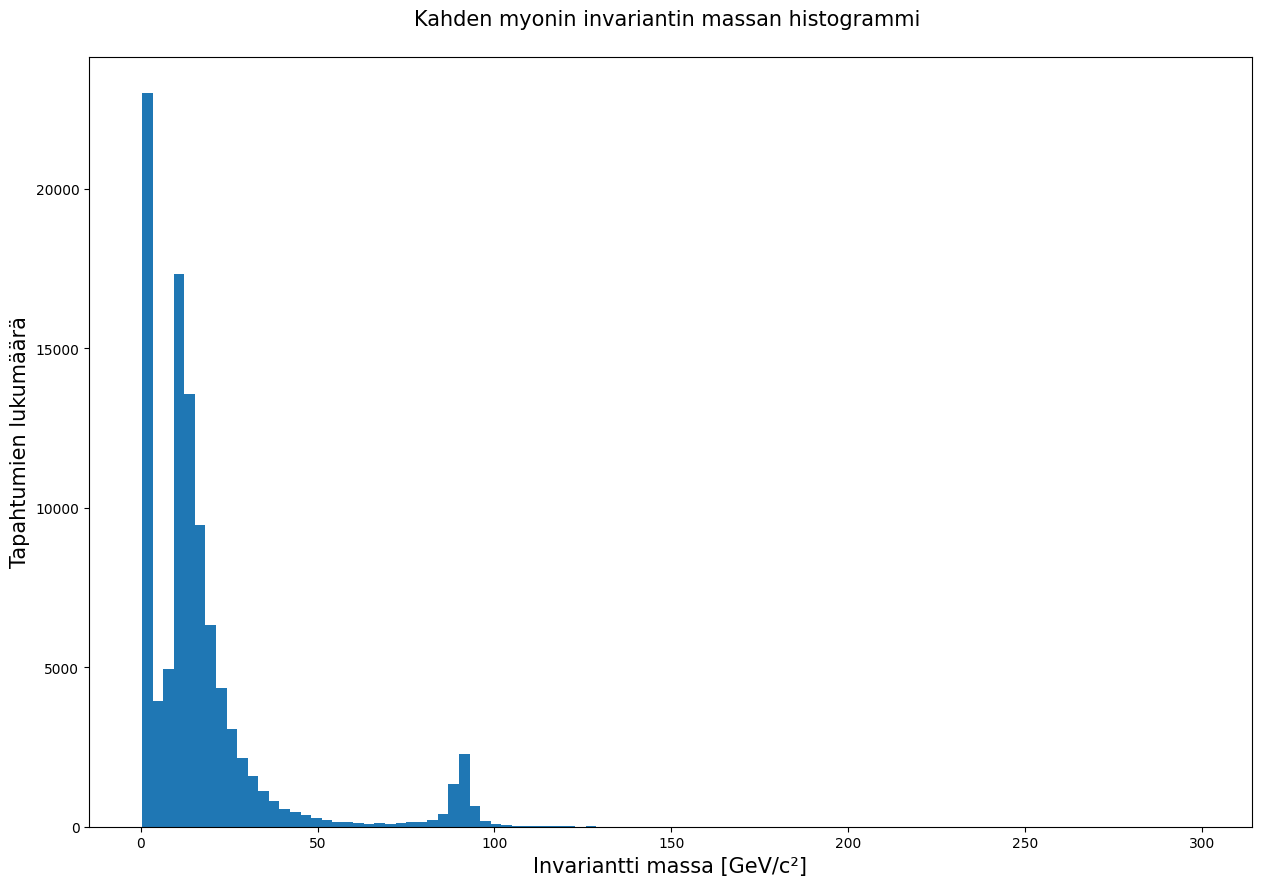
Signaalista nähdään monia asioita, mutta tarkastellaan yhtä kiinnostavaa huippua 80-100 GeVin kieppeillä rajaamalla kuvaajaa.

# Suoritetaan histogrammin piirtäminen:

fig = plt.figure(figsize = (15, 10))
plt.hist(kaksoismyonit.M, bins = 300, range = (80,100))

# Näillä riveillä ainoastaan määritellään otsikko sekä akseleiden tekstit.

plt.xlabel('Invariantti massa [GeV/c²]', fontsize = 15)
plt.ylabel('Tapahtumien lukumäärä', fontsize = 15)
plt.title('Kahden myonin invariantin massan histogrammi \n', fontsize = 15) # \n luo uuden rivin otsikon muotoilua varten

# Tehdään kuvaaja näkyväksi.

plt.show()

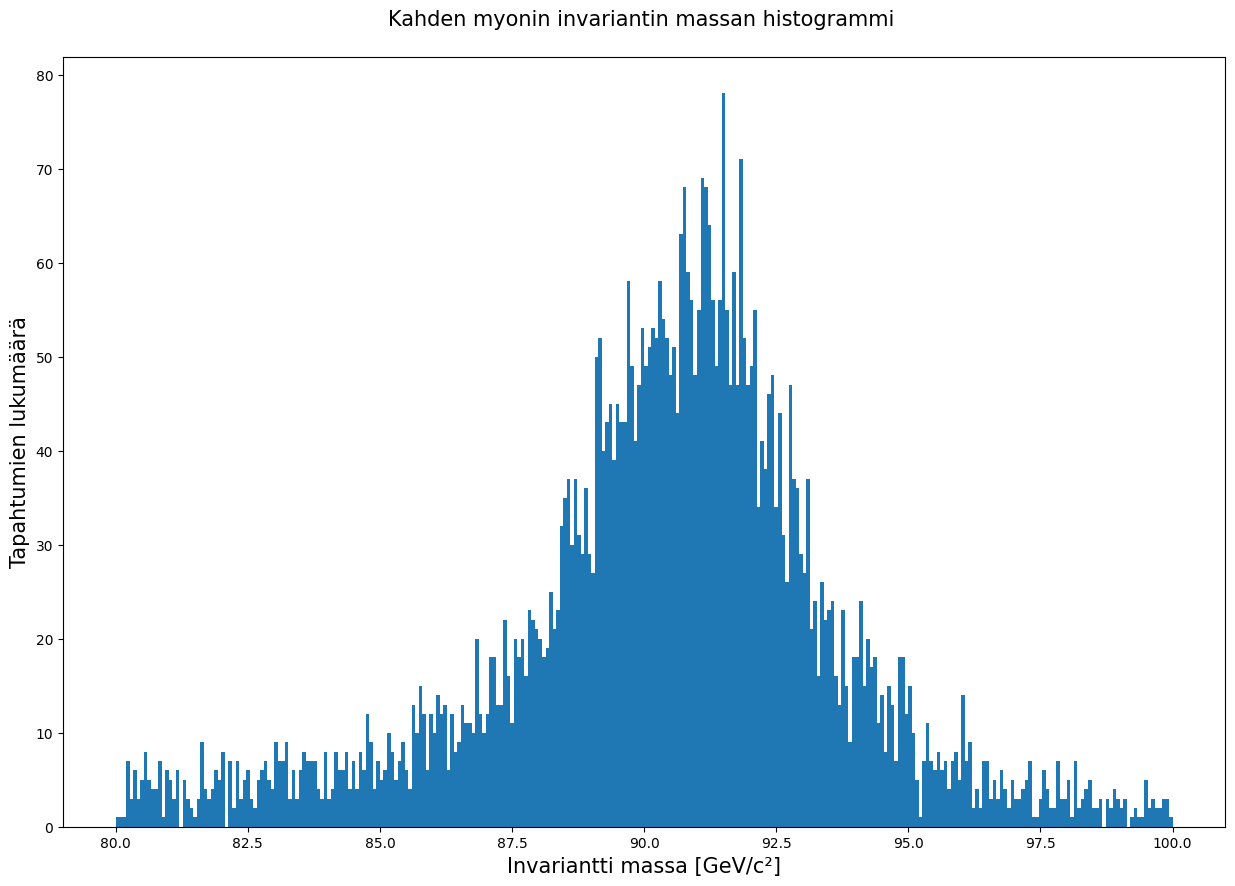
Tästä nähdään, että piikki sijoittuu noin 91 GeVin hujakoille, eli myonien taustalta löytynee Z-bosoni.

# Suoritetaan histogrammin piirtäminen myös J/psille.

fig = plt.figure(figsize = (15, 10))
plt.hist(jpsi.M, bins = 300)

# Näillä riveillä ainoastaan määritellään otsikko sekä akseleiden tekstit.

plt.xlabel('Invariantti massa [GeV/c²]', fontsize = 15)
plt.ylabel('Tapahtumien lukumäärä', fontsize = 15)
plt.title('J/$\psi$:n metsästys \n', fontsize = 15) # \n luo uuden rivin otsikon muotoilua varten

# Tehdään kuvaaja näkyväksi.

plt.show()

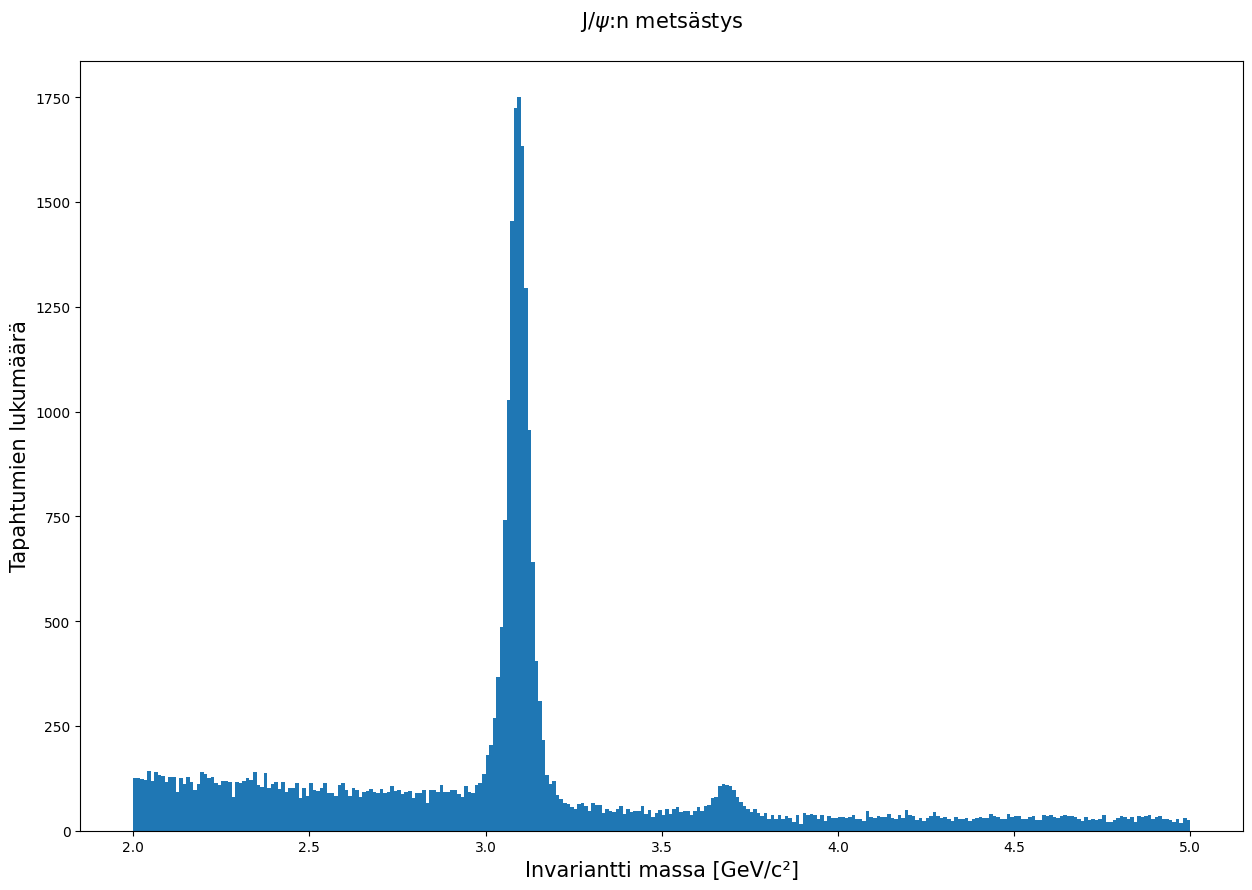
# Vastaavasti puristettuna kiinnostavampaan piikkiin.

fig = plt.figure(figsize = (15, 10))
plt.hist(jpsi.M, bins = 50, range = (3,3.2))

# Näillä riveillä ainoastaan määritellään otsikko sekä akseleiden tekstit.

plt.xlabel('Invariantti massa [GeV/c²]', fontsize = 15)
plt.ylabel('Tapahtumien lukumäärä', fontsize = 15)
plt.title('J/$\psi$:n metsästys \n', fontsize = 15) # \n luo uuden rivin otsikon muotoilua varten

# Tehdään kuvaaja näkyväksi.

plt.show()

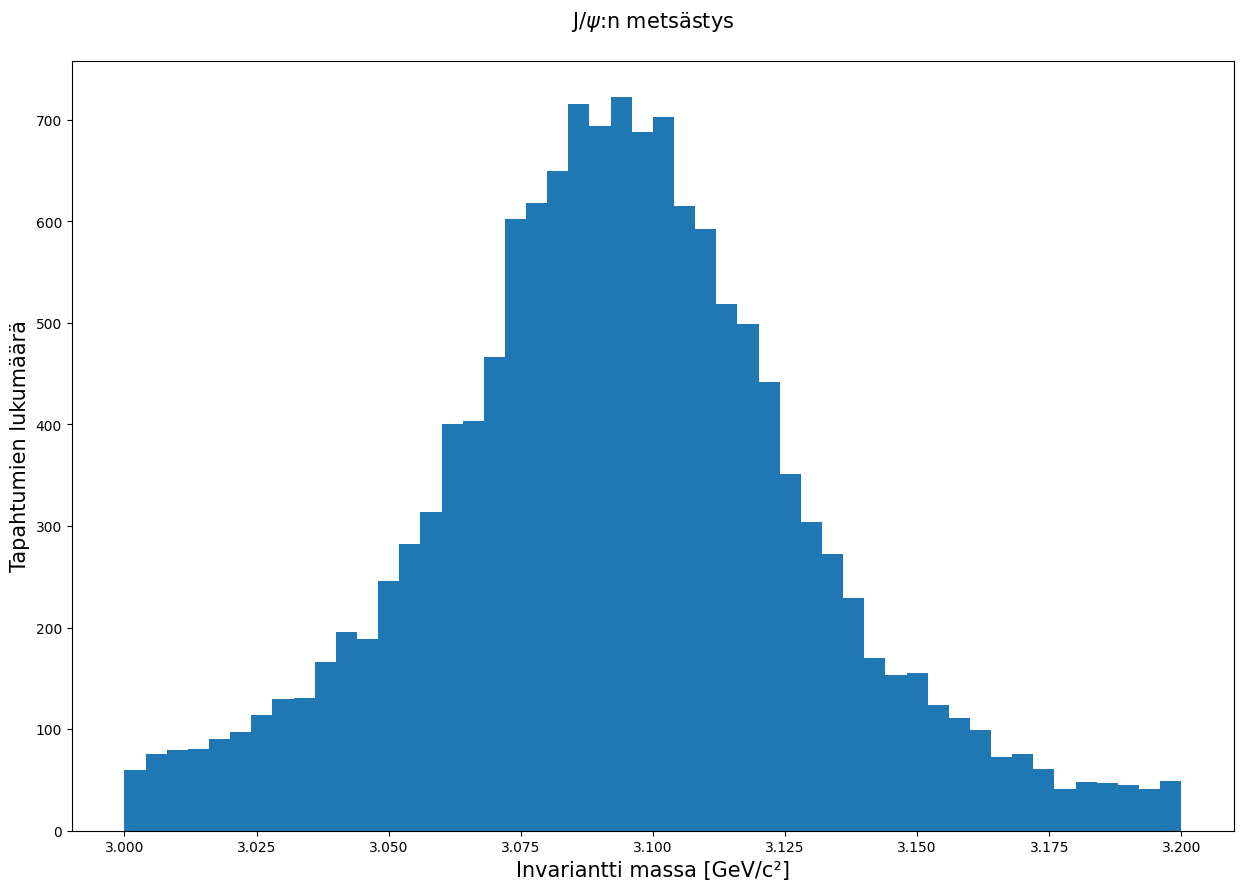
3. Jaottelu ja vertailu

Joskus on kiinnostavaa tarkastella miten eri osat datasta vaikuttavat lopputulokseen. Kokeillaan tässä jakaa dataa sen mukaan, oliko havaituilla hiukkasilla korkea vai matala energia.

ehto = 150

KorkeaEnergia = kaksoismyonit[(kaksoismyonit.E1 + kaksoismyonit.E2) >= ehto]
MatalaEnergia = kaksoismyonit[(kaksoismyonit.E1 + kaksoismyonit.E2) < ehto]

fig = plt.figure(figsize = (15, 10))
plt.hist(KorkeaEnergia.M, bins = 300, range = (80,100), alpha = 0.5, label = 'Korkea E', facecolor = 'k')
plt.hist(MatalaEnergia.M, bins = 300, range = (80,100), alpha = 0.5, label = 'Matala E')

plt.xlabel('Invariantti massa [GeV/c²]', fontsize = 15)
plt.ylabel('Tapahtumien lukumäärä', fontsize = 15)
plt.title('Kahden myonin invariantin massan histogrammi \n', fontsize = 15)
plt.legend (loc = 'upper right')

plt.show()

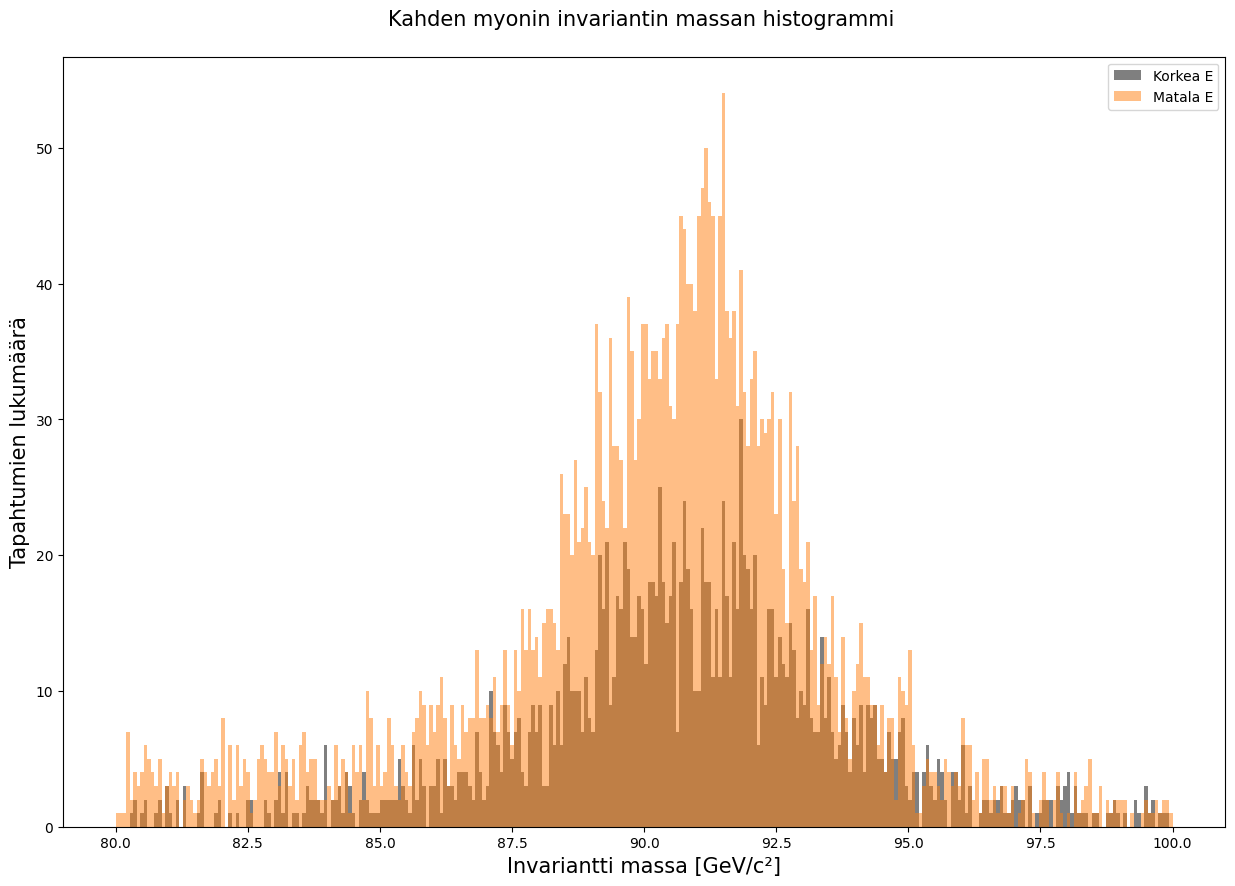
Näyttäisi siltä, että matalaenergisissä tapauksissa syntyisi enemmän kiinnostavia tapahtumia, mutta tässä on pidettävä mielessä histogrammin toimintaperiaate. Pikainen tarkastus kertoo monestako tapahtumasta kumpikin kuvaaja on koostettu.

print (len(KorkeaEnergia))
print (len(MatalaEnergia))

2106
97894

Mitenhän käy, jos jakoehdoksi laittaa vaikkapa 90 GeV? Mitä havaitaan, jos histogrammin alue alkaisikin jo matalasta päästä?

4. Pseudorapiditeetti

Pseudorapiditeetti $\eta$ (eetta) kuvaa havaitun hiukkasen poikkeamaa hiukkassuihkun suunnasta. Suuret, yli 2,5 arvot menevät niin suihkua pitkin, ettei niitä juurikaan saada mitattua, kun taas nollaa lähestyvät jäävät tarkimmin havainnointilaitteistoihin törmäysputken ympärillä.

Pseudorapiditeetista $\eta \equiv -ln[tan\frac{\theta}{2}]$ saadaan myös näkyviin törmäystapahtumien kulmajakauma, mikäli se auttaa hahmottamaan tilannetta.

Viereisessä kuvassa ajatellaan hiukkassuihkun kulkevan vaakasuuntaisesti vasemmalta oikealle.

prapMyonit = pd.concat([kaksoismyonit['eta1'],kaksoismyonit['eta2']])
prapJpsi = pd.concat([jpsi.eta1,jpsi.eta2])

kulmatMyonit = prapMyonit.copy()
kulmatMyonit[:] = [2*np.arctan(np.exp(x))*360/(2*np.pi) for x in kulmatMyonit]

kulmatJpsi = prapJpsi.copy()
kulmatJpsi[:] = [2*np.arctan(np.exp(x))*360/(2*np.pi) for x in kulmatJpsi]

fig = plt.figure(figsize = (15, 10))
plt.hist(prapMyonit, bins = 100, range = (-3,3))

plt.xlabel('Pseudorapiditeetti', fontsize = 15)
plt.ylabel('Tapahtumien lukumäärä', fontsize = 15)
plt.title('Jakauma \n', fontsize = 15)

plt.show()

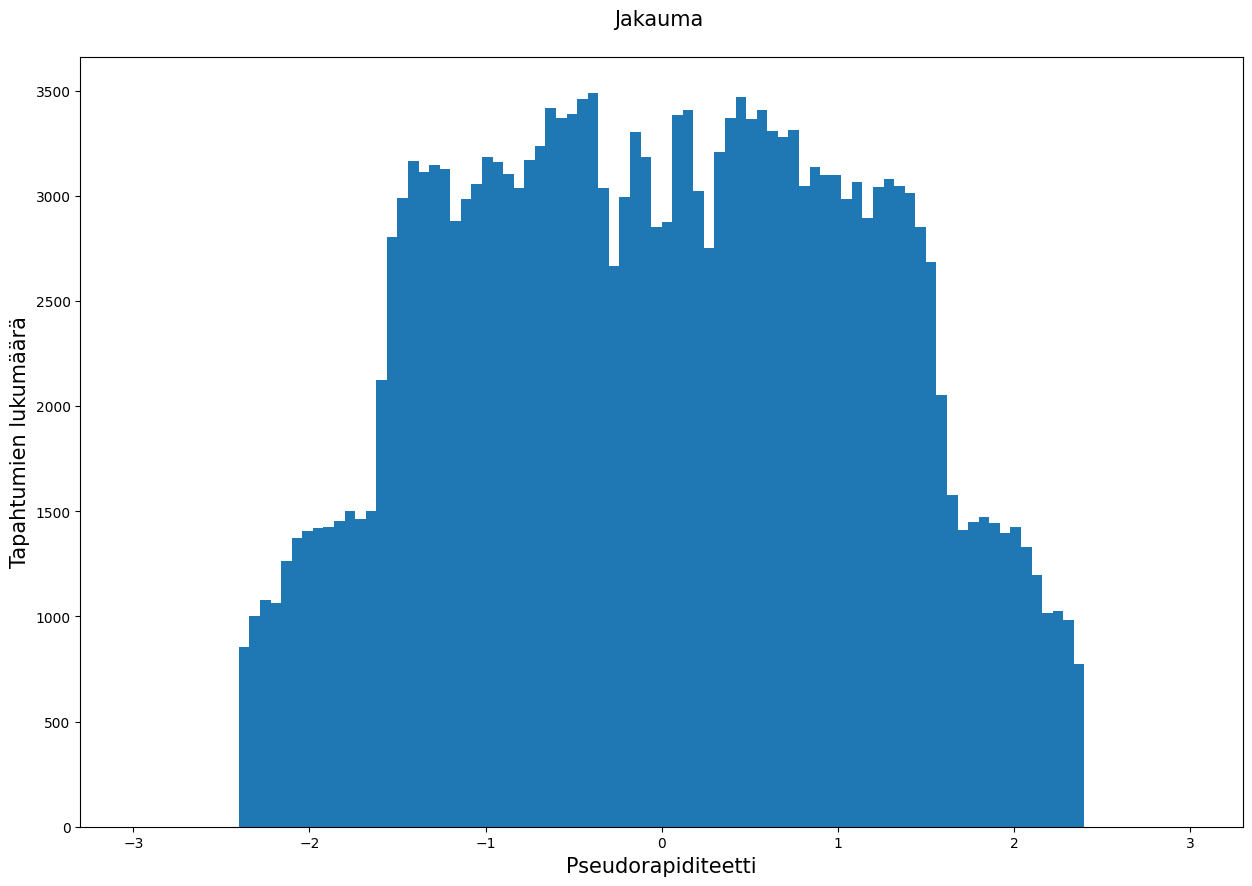
fig = plt.figure(figsize = (15, 10))
plt.hist(kulmatMyonit, bins = 180, range = (0,180))

plt.xlabel('Kulma (deg)', fontsize = 15)
plt.ylabel('Tapahtumien lukumäärä', fontsize = 15)
plt.title('Jakauma \n', fontsize = 15)

plt.show()

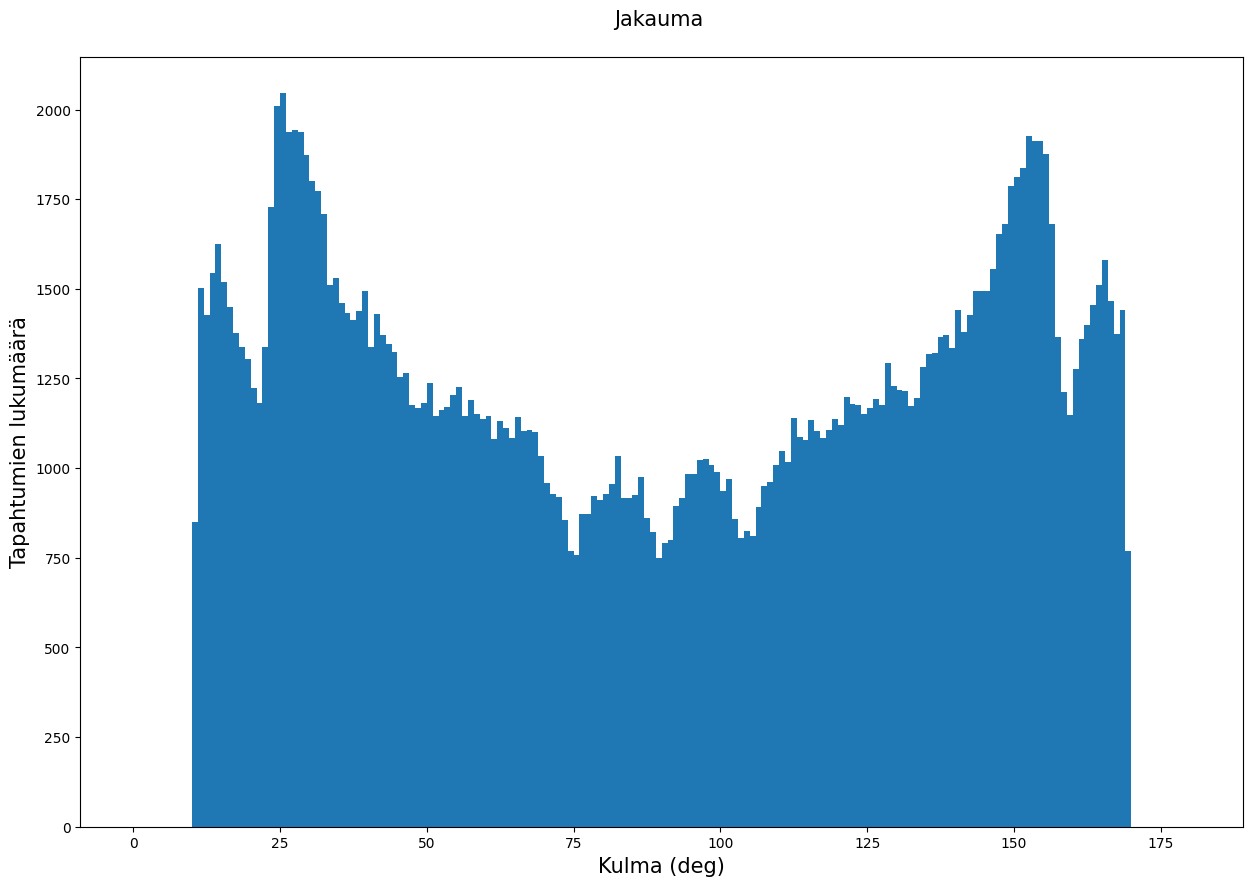
Kuvaajissa on selkeitä symmetrisiä muotoja. Mistähän moinen voisi johtua?

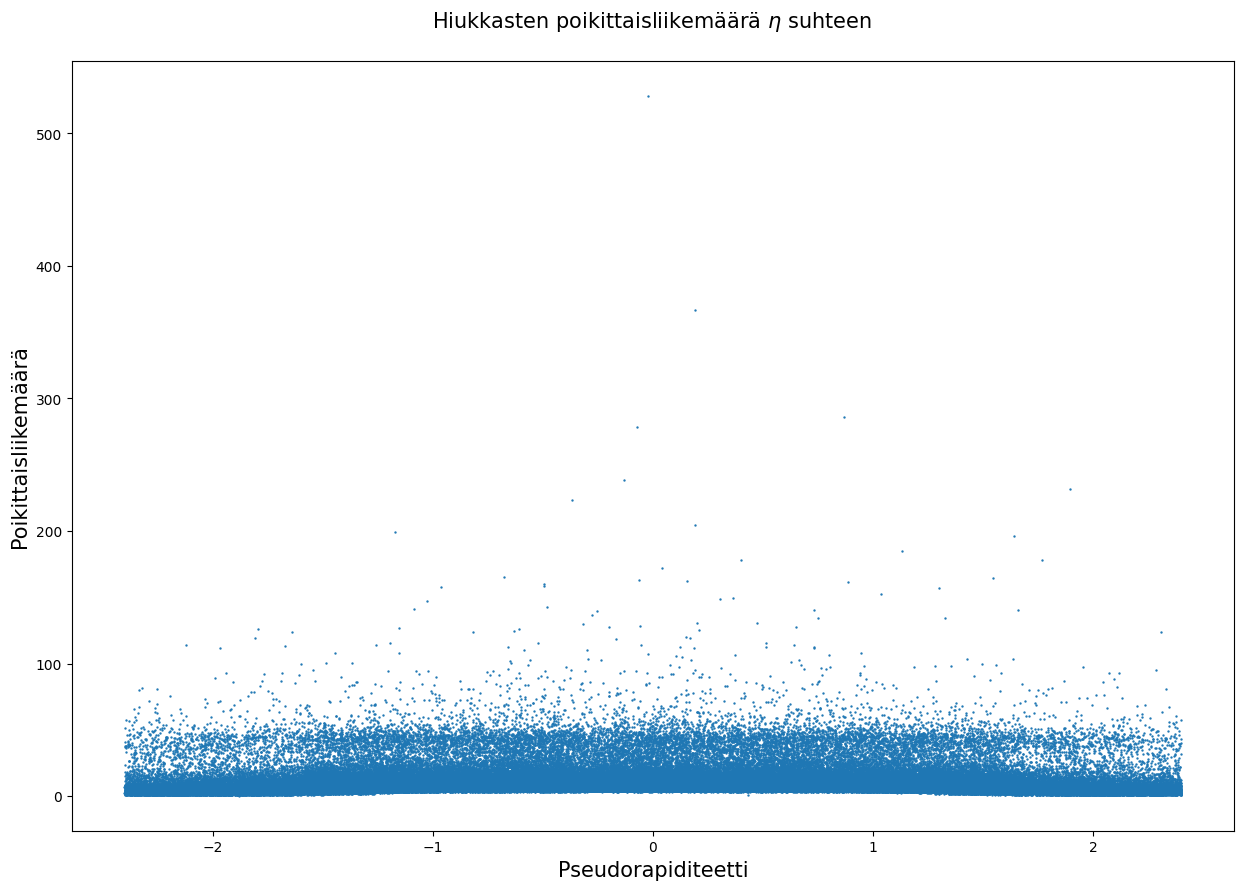
Hiukkasilla on poikittaista liikemäärää $p_T$. Mistähän voisi johtua seuraava pseudorapiditeetin ja $p_T$:n välinen suhde?

fig = plt.figure(figsize = (15, 10))
poikittaiset = pd.concat([kaksoismyonit.pt1,kaksoismyonit.pt2])
plt.scatter(prapMyonit, poikittaiset, s = 0.5)

#plt.ylim(0,6) # aja solu ensin niin, että tämä rivi on kommentti. Poista sitten ensimmäinen risuaita ja aja uudestaan.

plt.title('Hiukkasten poikittaisliikemäärä $\eta$ suhteen \n', fontsize = 15)
plt.xlabel('Pseudorapiditeetti', fontsize = 15)
plt.ylabel('Poikittaisliikemäärä', fontsize = 15)

plt.show()

5. Resoluutio

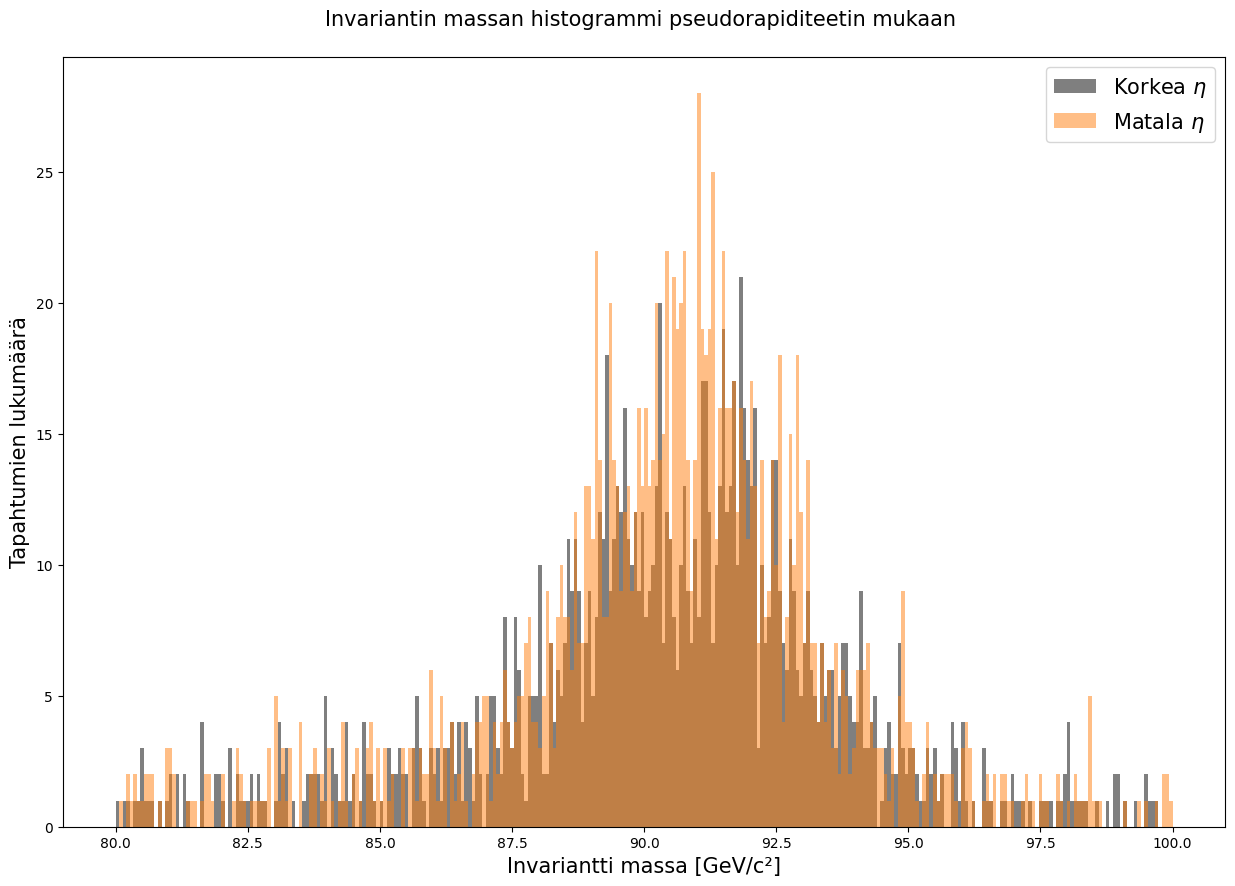
Pseudorapiditeetti määrittää havainnoitujen hiukkasten suuntaa, joka osaltaan kertoo miten tarkkoja tuloksia voidaan saada. Teknisistä syistä $\eta = \left | 2,5 \right |$ on suunnilleen äärirajalla mittalaitteiden asemoinnin suhteen. Mitä keskemmälle mitta-asemaa havainnot tulevat, sitä tarkemmin niistä voidaan sanoa jotakin, kuten nähdään seuraavista kuvaajista.

korkea = 1

suuret_eetat = kaksoismyonit[(abs(kaksoismyonit.eta1) >= korkea) & (abs(kaksoismyonit.eta2) >= korkea)]
pienet_eetat = kaksoismyonit[(abs(kaksoismyonit.eta1) < korkea) & (abs(kaksoismyonit.eta2) < korkea)]

fig = plt.figure(figsize = (15, 10))
plt.hist(suuret_eetat.M, bins = 300, range = (80,100), alpha = 0.5, label = 'Korkea $\eta$', facecolor = 'black')
plt.hist(pienet_eetat.M, bins = 300, range = (80,100), alpha = 0.5, label = 'Matala $\eta$')

plt.xlabel('Invariantti massa [GeV/c²]', fontsize = 15)
plt.ylabel('Tapahtumien lukumäärä', fontsize = 15)
plt.title('Invariantin massan histogrammi pseudorapiditeetin mukaan \n', fontsize = 15)
plt.legend (loc = 'upper right', fontsize = 15)

plt.show()

print (len(suuret_eetat))
print (len(pienet_eetat))

27672
34173

6. Sovitusta ja tilastoja

Suurten aineistojen käsittely kuvaajina auttaa niiden hahmottamisessa, mutta kuvien ohella tietokoneet ovat hyviä ilmiöitä kuvaavien sovitteiden etsimiseen sekä tilastollisten termien esiinkaivamiseen. Pythonissa on sisäänrakennettuja toimintoja esimerkiksi keskiarvojen, varianssin tai keskihajonnan laskemiseksi. Moneen havaintojoukkoon voi koettaa sovittaa tyypillisiä perusjakaumia, kuten normaalijakaumaa.

alaraja = 87
ylaraja = 95

pala = kaksoismyonit[(kaksoismyonit.M > alaraja) & (kaksoismyonit.M < ylaraja)]

fig = plt.figure(figsize = (15, 10))

esite_ala = 80
esite_yla = 100

alue = kaksoismyonit[(kaksoismyonit.M > esite_ala) & (kaksoismyonit.M < esite_yla)]

kerroin = len(pala)/len(alue)
(mu, sigma) = norm.fit(pala.M)

n, bins, patches = plt.hist(kaksoismyonit.M, 300, density = 1, facecolor = 'green', alpha = 0.75, histtype = 'stepfilled',
                            range = (esite_ala,esite_yla))

y = kerroin*norm.pdf( bins, mu, sigma)
l = plt.plot(bins, y, 'r--', linewidth = 2)

plt.xlabel('Massa [GeV/$c^2$]', fontsize = 15)
plt.ylabel('Tapahtuman todennäköisyys', fontsize = 15)
plt.title(r'$\mathrm{Histogrammi\ invarianteista\ massoista\ normeerattuna\ ykköseen:}\ \mu=%.3f,\ \sigma=%.3f$'
          %(mu,sigma),fontsize=15)
plt.grid(True)

plt.show()

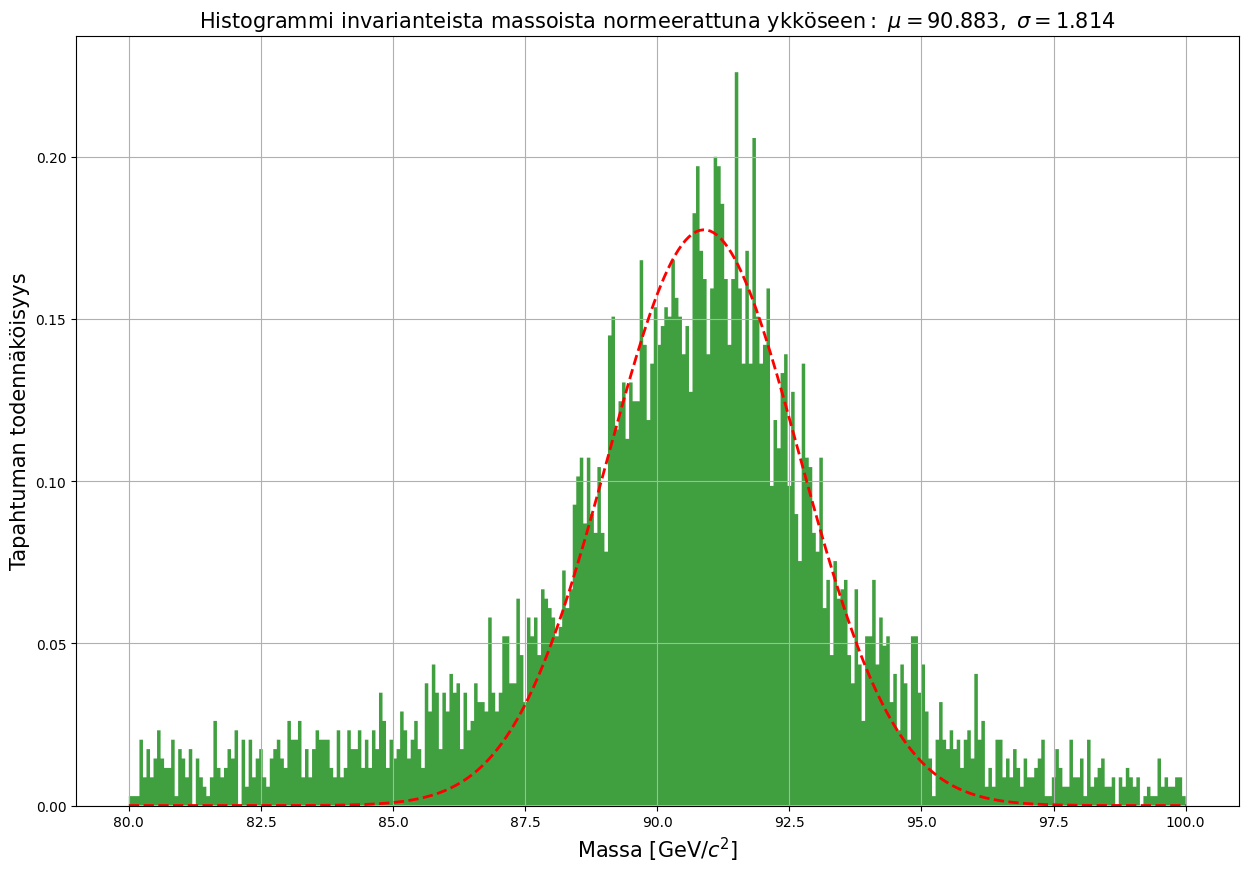
Hiukkasfysiikan tarpeisiin normaalijakauma on kuitenkin väärä työkalu, vaikka satunnaisesti näyttäisikin soveltuvan yksittäisiin paikkoihin. Poisson-jakauma olisi asteen parempi, mutta tyypillisesti käytetään Breit-Wigner -jakaumaa:

$$ N(E) = \frac{K}{(E-M)^2 + \frac{\Gamma^2}{4}} $$

jossa $E$ on energia, $M$ piikin huippukohta, $\Gamma$ jakauman luonnollinen leveys ja $K$ vakio. Resonanssissa havaitun hiukkasen elinaika $\tau$ liittyy jakauman leveyteen seuraavasti:

$$ \Gamma \equiv \frac{\hbar}{\tau} $$

Voit kokeilla B-W-sovitusta alla eri kohtiin aineistoa. Rajojen siirtäminen vaatii myös alkuarvojen huippukohdan siirtämistä.

# Ensin määritetään tarkastelualueen rajat ja tarkkuus.

lowerlimit = 2
upperlimit = 4
bins = 100

# Haetaan aineisto. 

ds = pd.read_csv(
    'https://raw.githubusercontent.com/cms-opendata-education/cms-jupyter-materials-finnish/master/Data/Dimuon_DoubleMu.csv')
i_mass = ds.M
hist, edges = np.histogram(i_mass, bins = 100, range = (lowerlimit, upperlimit))

# Määritetään funktio jakaumalle.

def breitwigner(E, gamma, M, a, b, A):
    return a*E+b+A*( (2*np.sqrt(2)*M*gamma*np.sqrt(M**2*(M**2+gamma**2)))/(np.pi*np.sqrt(M**2+np.sqrt(M**2*(M**2+gamma**2)))) )/((E**2-M**2)**2+M**2*gamma**2)

from scipy.optimize import curve_fit

# Annetaan koneelle alkuarvot ja iteroidaan pari kertaa parantaen sovitusta.

#initials = [1, 91, -1, 200, 13000] # Z-bosonille 90 GeVin kieppeillä
initials = [1, 3.1, -1, 100, 13000] # J/psi 3 GeVin kieppeillä
x = np.linspace(lowerlimit, upperlimit, bins)
y = hist

i = 0
while i < 5:
    popt, pcov = curve_fit(breitwigner, x, y, p0 = initials, sigma = np.sqrt(y))
    i = i+1
    initials = popt
    #print(initials) for checking up
    
error = np.sqrt(np.diag(pcov)) 

# Piirretään kuvaajat ja printataan tilastolliset tiedot näkyviin.

plt.figure(figsize = (10,5))
plt.hist(i_mass, bins, range = (lowerlimit,upperlimit), label = "Alkuperäinen histogrammi", alpha = 0.5 )
plt.plot(x, breitwigner(x, *popt), color = 'r', label = "Breit-Wigner -sovitus")
plt.scatter(x,y, color = 'b', label = "")
plt.legend(loc = "upper right")
plt.xlabel("\n Invariantti massa (GeV)", fontsize = 15)
plt.ylabel("Tapahtumien lukumäärä \n", fontsize = 15)
plt.title("Hiukkanen on hajonnut kahdeksi myoniksi \n", fontsize = 15)
plt.show()

print("Tämän hiukkasen massa on: " + str(popt[1])+ u" \u00B1 " + str(error[1]) + " GeV")

tau_high = 1/(popt[0]-error[0])
tau_low = 1/(popt[0]+error[0])
var = (tau_high - tau_low)/2
tau = tau_high - var

print("Tämän hiukkasen elinaika on: " + str(tau) + u" \u00B1 " + str(var) + " GeV^-1" )

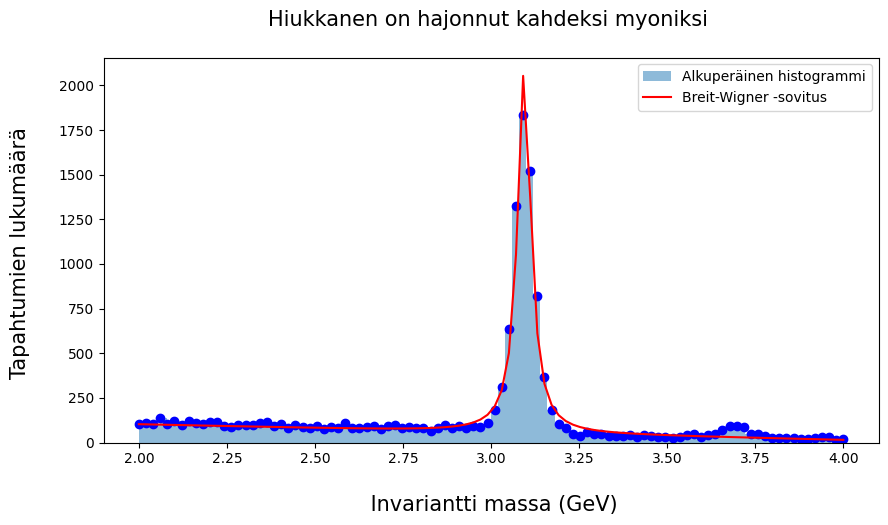
Tämän hiukkasen massa on: 3.0942088781215977 ± 0.001210341006419428 GeV
Tämän hiukkasen elinaika on: 21.865056540308995 ± 1.1700486803971408 GeV^-1