Higgsiä metsästämässä - esimerkki tutkimuksesta#
Tässä harjoitteessa käydään läpi miten Higgsin bosonia etsittiin ja miten tieteellinen tutkimus usein toimii.
Käytetty data on aitoa, merkityksellistä mittausdataa kokeista, joissa Higgsin bosonin olemassaolo todistettiin. Tätä seurasikin sitten pian Nobelin palkinto. Nyt tuo data on myös sinun tutkittavanasi sen sijaan, että se piilottelisi jossain valmiiden kuvien takana.
Metodi on hyvin yleispätevä ja käytössä monilla tieteenaloilla. Kun meillä on jonkinlaista teoriapohjaa, voimme tehdä mittauksia ja vertailla tuloksia oletuksiimme. Ehkäpä tulokset vahvistavat odotuksemme, kenties niistä nousee uusia kysymyksiä, voi olla että joudumme korjaamaan teorioitamme tai jopa kehittämään aivan uusia selittääksemme havainnot. Tämä sykli sitten toistuu uudelleen ja uudelleen porautuessamme syvemmälle luonnon toimintaan.
Aloitetaanpa Higgsin bosonin metsästys!
# Tuodaan tarvittavat paketit
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Tässä haetaan CERN:n avoin data portaalista useita eri datatiedostoja
# Mitä enemmän dataa, sitä varmempia tuloksia Higgsin löytymisestä voimme saada!
# Tähän dataan palataan pian.
csvs = [pd.read_csv('http://opendata.cern.ch/record/5200/files/4mu_2011.csv'), pd.read_csv('http://opendata.cern.ch/record/5200/files/4e_2011.csv'), pd.read_csv('http://opendata.cern.ch/record/5200/files/2e2mu_2011.csv')]
csvs += [pd.read_csv('http://opendata.cern.ch/record/5200/files/4mu_2012.csv'), pd.read_csv('http://opendata.cern.ch/record/5200/files/4e_2012.csv'), pd.read_csv('http://opendata.cern.ch/record/5200/files/2e2mu_2012.csv')]
fourlep = pd.concat(csvs)
Standardimallin ennusteiden mukaan Higgsin bosoni voi hajota mm. siten, että siitä syntyy ensin kaksi Z-bosonia ja niistä edelleen neljä leptonia (elektroneja, myoneja…). Neljä leptonia voi kuitenkin syntyä myös monista muista prosesseista, jotka vaikeuttavat tehtäväämme Higgsin bosonin metsästyksessä. Nämä muut prosessit ovat analyysissämme siis taustakohinaa, josta meidän tulisi erottaa ne prosessit, joissa Higgsin hiukkanen on ollut osallisena. Teoria itsessään ei kerro paljoakaan siitä, mikä Higgsin hiukkasen massa voisi olla, mutta valistuneilla arvauksilla päästään aika pitkälle. Esimerkiksi hiukkasen hajoaminen neljään leptoniin on todennäköisempää tietyillä massoilla, joten kohdistetaan etsintämme näihin massoihin.
Tarkoituksenamme on siis tutkia törmäyksessä syntyneille neljälle leptonille laskettua invarianttia massaa tekemällä usean törmäyksen datasta histogrammi.
# Tutkitaan sellaisia tapahtumia, joissa neljälle leptonille laskettu invariantti massa
# on välillä 70 GeV - 181 GeV
rmin = 70
rmax = 181
nbins = 37
hist, bins, patches = plt.hist(fourlep['M'], bins = nbins, range = (rmin,rmax))
width = 1.0*(bins[1] - bins[0])
center = (bins[:-1] + bins[1:]) / 2
plt.xlabel('4l invariantti massa (GeV)', fontsize = 15)
plt.ylabel('Tapahtumia\n', fontsize = 15)
plt.show()
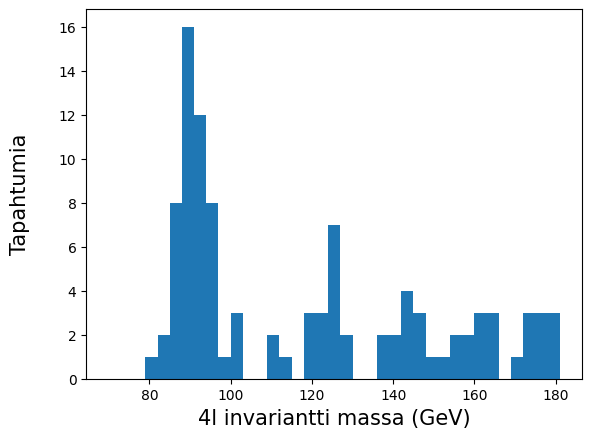
Histogrammissa näkyy joitakin massan alueita, joissa on enemmän tapahtumia kuin muissa, mutta emme pysty kuitenkaan tekemään varmoja johtopäätöksiä Higgsin olemassaolosta tästä kuvasta.
Otetaan tutkimuksemme avuksi simulaatioita. Jos tunnemme joitain prosesseja, joita törmäyksissä tapahtuu, voimme vertailla niiden odotettavia tuloksia varsinaisiin mittauksiimme. Alla on Monte Carlo-menetelmillä tuotettuja arvoja, jotka on painotettu luminositeetin, poikkileikkauksen ja tapahtumien määrän mukaan. Periaatteessa niissä on siis luotu satunnaisvaihtelulla maustettua dataa, jollaista voisi saada oikeastakin mittauksesta, niin että kyseinen joukko noudattaa samanlaista jakaumaa kuin kyseisen prosessin on mitattu tuottavan.
Simulaatiodata vastaa siis eri “hajoamiskanavista” peräisin olevien neljän leptonin massajakaumia.
dy = np.array([0,0,0,0,0,0.354797,0.177398,2.60481,0,0,0,0,0,0,0,0,0,0.177398,0.177398,0,0.177398,0,0,0,0,0,0,0,0,0,0,0,0.177398,0,0,0,0])
ttbar = np.array([0.00465086,0,0.00465086,0,0,0,0,0,0,0,0.00465086,0,0,0,0,0,0.00465086,0,0,0,0,0.00465086,0.00465086,0,0,0.0139526,0,0,0.00465086,0,0,0,0.00465086,0.00465086,0.0139526,0,0])
zz = np.array([0.181215,0.257161,0.44846,0.830071,1.80272,4.57354,13.9677,14.0178,4.10974,1.58934,0.989974,0.839775,0.887188,0.967021,1.07882,1.27942,1.36681,1.4333,1.45141,1.41572,1.51464,1.45026,1.47328,1.42899,1.38757,1.33561,1.3075,1.29831,1.31402,1.30672,1.36442,1.39256,1.43472,1.58321,1.85313,2.19304,2.95083])
hzz = np.array([0.00340992,0.00450225,0.00808944,0.0080008,0.00801578,0.0108945,0.00794274,0.00950757,0.0130648,0.0163568,0.0233832,0.0334813,0.0427229,0.0738129,0.13282,0.256384,0.648352,2.38742,4.87193,0.944299,0.155005,0.0374193,0.0138906,0.00630364,0.00419265,0.00358719,0.00122527,0.000885718,0.000590479,0.000885718,0.000797085,8.86337e-05,0.000501845,8.86337e-05,0.000546162,4.43168e-05,8.86337e-05])
Vilkaistaas millaisia muotoja nämä tuottavat ja miten ne suhtautuvat kiihdyttimessä mitattuihin tuloksiin.
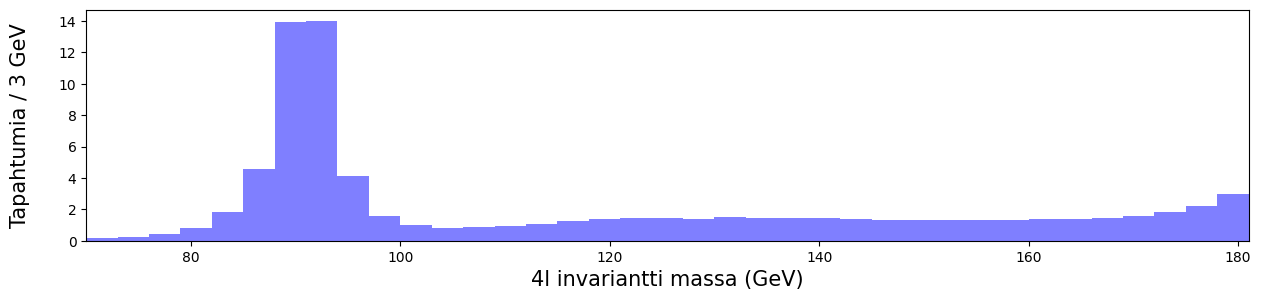
# ZZ, pari raskaampaa bosonia.
plt.figure(figsize = (15,3))
plt.bar(center, zz, align = 'center', width = width, color = 'b', linewidth = 0, edgecolor = 'black', alpha = 0.5)
plt.xlabel('4l invariantti massa (GeV)', fontsize = 15)
plt.ylabel('Tapahtumia / 3 GeV\n', fontsize = 15)
plt.xlim(rmin,rmax)
plt.show()
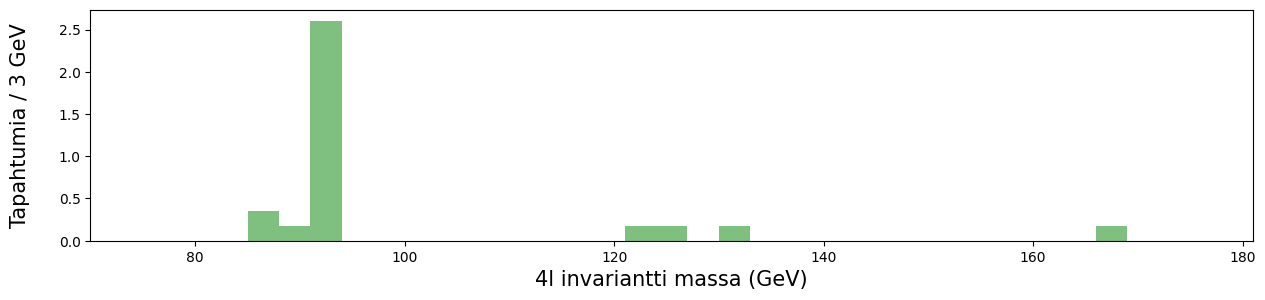
# DY, yksittäisistä Z-bosoneista koostuvia tapahtumia.
plt.figure(figsize = (15,3))
plt.bar(center, dy, align = 'center', width = width, color = 'g', linewidth = 0, edgecolor = 'black', alpha = 0.5)
plt.xlabel('4l invariantti massa (GeV)', fontsize = 15)
plt.ylabel('Tapahtumia / 3 GeV\n', fontsize = 15)
plt.xlim(rmin,rmax)
plt.show()
# ttbar, top- ja antitopkvarkkien pari.
plt.figure(figsize = (15,3))
plt.bar(center, ttbar, align = 'center', width = width, color = 'gray', linewidth = 0, edgecolor = 'b', alpha = 0.5)
plt.xlabel('4l invariantti massa (GeV)', fontsize = 15)
plt.ylabel('Tapahtumia / 3 GeV \n', fontsize = 15)
plt.xlim(rmin,rmax)
plt.show()
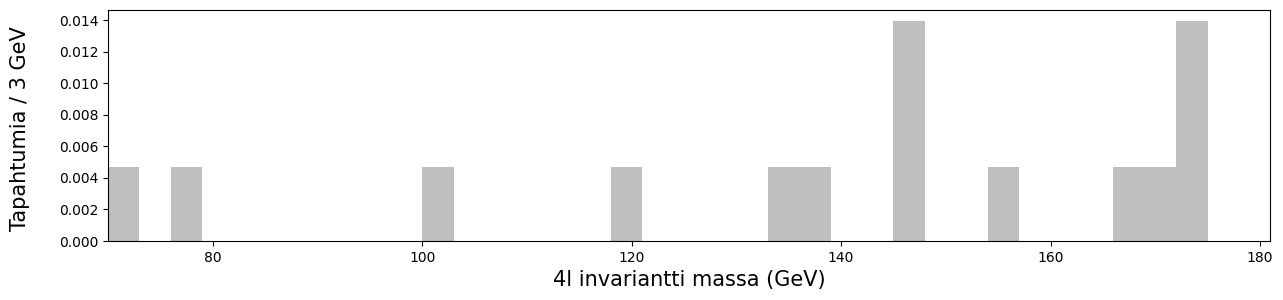
Lyödään askeiset päällekäin ja tarkastellaan, miltä voisimme olettaa tulostemme näyttävän.
plt.figure(figsize = (15,5))
# ttbar
ttbar_bar = plt.bar(center, ttbar, align = 'center', width = width, color = 'gray', linewidth = 0, edgecolor = 'b',
alpha = 0.5, label = r'$t\bar{t}$')
# DY
dy_bar = plt.bar(center, dy, align = 'center', width = width, color = 'g', linewidth = 0, edgecolor = 'black',
alpha = 0.5, bottom = ttbar, label = 'Z/$\gamma^{*}$ + X')
# ZZ
zz_bar = plt.bar(center, zz, align = 'center', width = width, color = 'b', linewidth = 0, edgecolor = 'black',
alpha = 0.5, bottom = ttbar+dy, label = r'ZZ $\rightarrow$ 4l')
plt.title('$ \sqrt{s} = 7$ TeV, L = 2.3 $fb^{-1}$; $\sqrt{s} = 8$ TeV, L = 11.6 $fb^{-1}$ \n', fontsize = 12)
plt.xlabel('$m_{4l}$ (GeV)', fontsize = 15)
plt.ylabel('Tapahtumia / 3 GeV\n', fontsize = 15)
plt.ylim(0,25)
plt.xlim(rmin,rmax)
plt.legend(fontsize = 15)
plt.show()
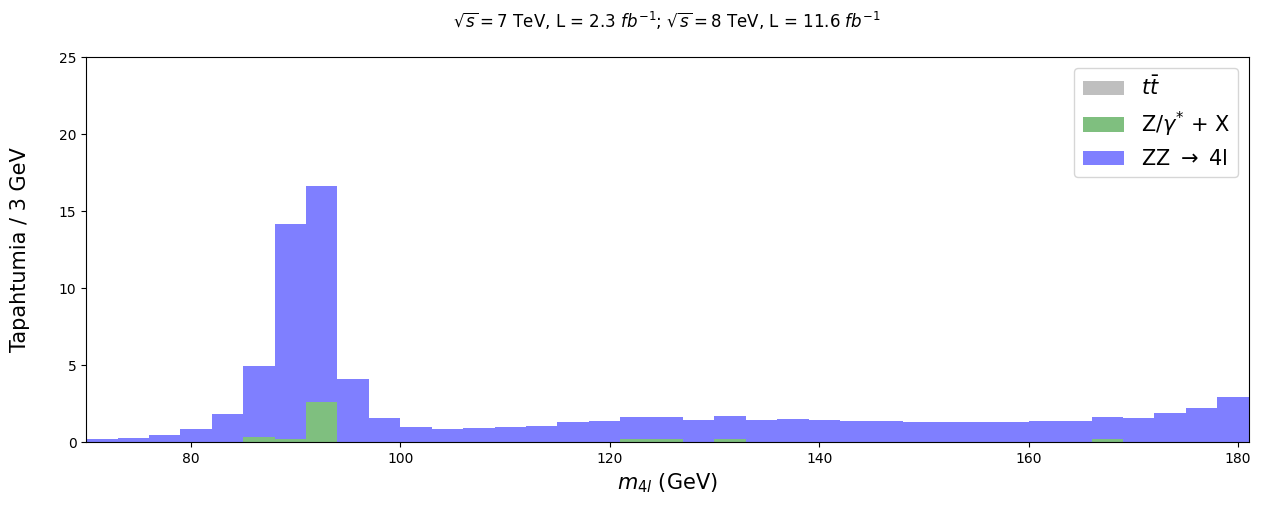
Selvästi ainakin 90 GeVin tietämillä on tapahtumia, mikä käy järkeen huomioiden suurimman osan tuloksista syntyvän Z-bosonien kautta, joiden massa on noin 90 GeV. Otetaanpa sitten mukaan myös itse mittaukset. Miten hyvin kuvat vastaavat toisiaan?
plt.figure(figsize = (15,5))
xerrs = [width*0.5 for i in range(0, nbins)]
yerrs = np.sqrt(hist)
# ttbar
ttbar_bar = plt.bar(center, ttbar, align = 'center', width = width, color = 'gray', linewidth = 0, edgecolor = 'b',
alpha = 0.5, label = r'$t\bar{t}$')
# DY
dy_bar = plt.bar(center, dy, align = 'center', width = width, color = 'g', linewidth = 0, edgecolor = 'black',
alpha = 0.5, bottom = ttbar, label = 'Z/$\gamma^{*}$ + X')
# ZZ
zz_bar = plt.bar(center, zz, align = 'center', width = width, color = 'b', linewidth = 0, edgecolor = 'black',
alpha = 0.5, bottom = ttbar+dy, label = r'ZZ $\rightarrow$ 4l')
# Mittaukset.
data_bar = plt.errorbar(center, hist, xerr = xerrs, yerr = yerrs, linestyle = 'None', color = 'black',
marker = 'o', label = 'Data')
plt.title('$ \sqrt{s} = 7$ TeV, L = 2.3 $fb^{-1}$; $\sqrt{s} = 8$ TeV, L = 11.6 $fb^{-1}$ \n', fontsize = 12)
plt.xlabel('$m_{4l}$ (GeV)', fontsize = 15)
plt.ylabel('Tapahtumia / 3 GeV\n', fontsize = 15)
plt.ylim(0,25)
plt.xlim(rmin,rmax)
plt.legend(fontsize = 15)
plt.show()
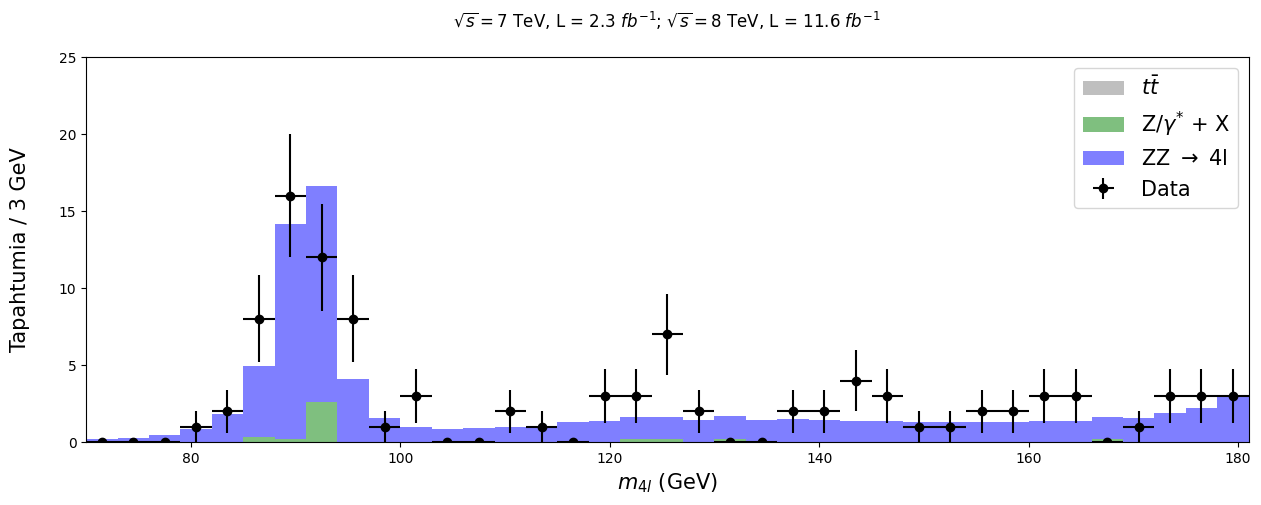
Kaikki mittapisteet eivät selvästikään selity tuntemillamme taustaprosesseilla. Vertailua varten fyysikot laskivat hajontoja Higgsin bosonille lähtien eri massaisista oletuksista. Tässä näytetään, millainen hajonta tuolla hiukkasella olisi, jos Higgsin massa olisi suunnilleen 125 GeV.
# HZZ, teoreettinen oletus Higgsin bosonin muodolle 125 GeVin kohdalla.
plt.figure(figsize = (15,3))
plt.bar(center, hzz, align = 'center', width = width, color = 'w', linewidth = 1, edgecolor = 'r')
plt.xlabel('4l invariantti massa (GeV)', fontsize = 15)
plt.ylabel('Tapahtumia / 3 GeV\n', fontsize = 15)
plt.xlim(rmin,rmax)
plt.show()
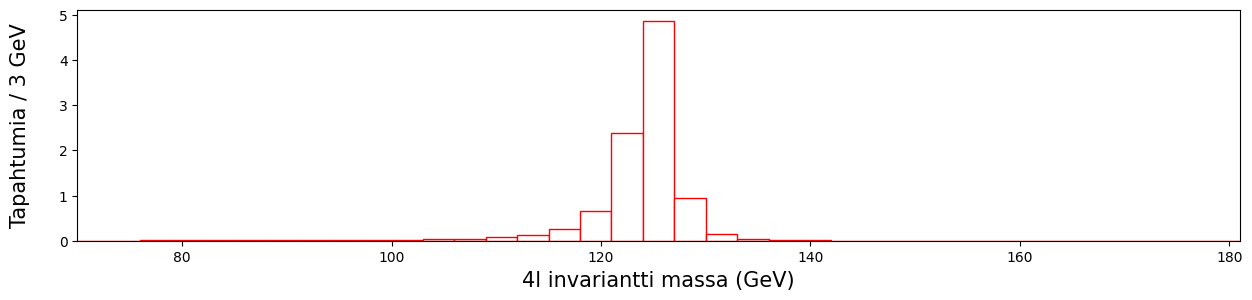
Bonuskysymys: miten jokin, jolla on 125 GeVin massa, voi hajota kahdeksi Z-bosoniksi, jonka massa on yli 90 GeViä?
Lisätääs tämäkin tulos kokonaiskuvaan.
plt.figure(figsize = (15,5))
# ttbar
ttbar_bar = plt.bar(center, ttbar, align = 'center', width = width, color = 'gray', linewidth = 0, edgecolor = 'b',
alpha = 0.5, label = r'$t\bar{t}$')
# DY
dy_bar = plt.bar(center, dy, align = 'center', width = width, color = 'g', linewidth = 0, edgecolor = 'black',
alpha = 0.5, bottom = ttbar, label = 'Z/$\gamma^{*}$ + X')
# ZZ
zz_bar = plt.bar(center, zz, align = 'center', width = width, color = 'b', linewidth = 0, edgecolor = 'black',
alpha = 0.5, bottom = ttbar+dy, label = r'ZZ $\rightarrow$ 4l')
# HZZ
hzz_bar = plt.bar(center, hzz, align = 'center', width = width, color = 'w', linewidth = 1, edgecolor = 'r',
bottom = ttbar+dy+zz, label = '$m_{H}$ = 125 GeV')
# Mittaukset.
data_bar = plt.errorbar(center, hist, xerr = xerrs, yerr = yerrs, linestyle = 'None', color = 'black',
marker = 'o', label = 'Data')
plt.title('$ \sqrt{s} = 7$ TeV, L = 2.3 $fb^{-1}$; $\sqrt{s} = 8$ TeV, L = 11.6 $fb^{-1}$ \n', fontsize = 12)
plt.xlabel('$m_{4l}$ (GeV)', fontsize = 15)
plt.ylabel('Tapahtumia / 3 GeV\n', fontsize = 15)
plt.ylim(0,25)
plt.xlim(rmin,rmax)
plt.legend(fontsize = 15)
plt.show()
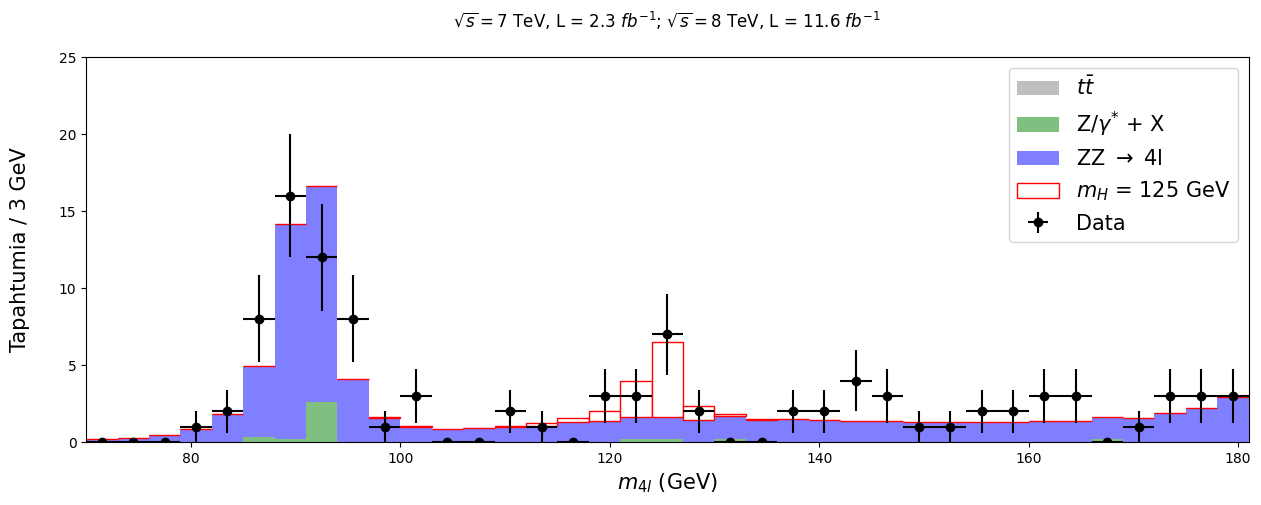
Otos vaikuttaa hitusen pieneltä, mitä se toki puhtaasti numeromäärältään onkin, mutta se antaa silti valaisevan vilkaisun siihen, kuinka tutkimustyötä tehdään. Kovin moni hajoamisprosessi ei tuota lopputilassa neljää leptonia, joten edes näin monen pisteen saaminen käsittää suunnilleen puolet kaikesta julkisesti saatavilla olevasta datasta vuoden 2011-2012 kokeesta. Lisäinfoa mittauksista voi löytää täältä.
# Jos dataa haluaa tarkastella lähemmin, siitä löytää tietoja kaikista havainnoiduista neljästä hiukkasesta.
pd.options.display.max_columns = 50
fourlep.head()
| Run | Event | PID1 | E1 | px1 | py1 | pz1 | pt1 | eta1 | phi1 | Q1 | PID2 | E2 | px2 | py2 | pz2 | pt2 | eta2 | phi2 | Q2 | PID3 | E3 | px3 | py3 | pz3 | pt3 | eta3 | phi3 | Q3 | PID4 | E4 | px4 | py4 | pz4 | pt4 | eta4 | phi4 | Q4 | mZ1 | mZ2 | M | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 173657 | 34442568 | 13 | 35.9978 | 32.7631 | -4.41922 | -14.2436 | 33.0598 | -0.418519 | -0.134075 | -1 | -13 | 29.0804 | -19.31050 | -5.31425 | 21.0837 | 20.0284 | 0.918146 | -2.873040 | 1 | 13 | 17.3154 | -10.87010 | -3.64596 | 12.9753 | 11.46530 | 0.971505 | -2.81797 | -1 | -13 | 11.49390 | -1.20978 | 11.35650 | 1.29029 | 11.42070 | 0.112739 | 1.676920 | 1 | 62.5513 | 20.5205 | 91.4517 |
| 1 | 166512 | 337493970 | 13 | 52.9826 | -49.9170 | 8.17082 | 15.7696 | 50.5813 | 0.306925 | 2.979340 | -1 | 13 | 72.1018 | 15.32840 | 21.35470 | -67.1392 | 26.2866 | -1.667150 | 0.948222 | -1 | -13 | 89.7552 | 10.34670 | -20.27240 | 86.8214 | 22.76010 | 2.048740 | -1.09888 | 1 | -13 | 30.21620 | 2.32913 | -13.06840 | 27.14400 | 13.27430 | 1.463510 | -1.394420 | 1 | 92.1352 | 90.2049 | 235.8800 |
| 2 | 171091 | 69105221 | 13 | 165.9750 | -12.6280 | -30.22890 | 162.7100 | 32.7605 | 2.305880 | -1.966510 | -1 | -13 | 68.1611 | 6.93837 | 22.85760 | 63.8382 | 23.8875 | 1.709440 | 1.276090 | 1 | -13 | 19.5056 | 4.71517 | 8.50412 | 16.9087 | 9.72383 | 1.320370 | 1.06454 | 1 | 13 | 24.83870 | -8.09683 | 3.05681 | 23.28190 | 8.65464 | 1.715610 | 2.780600 | -1 | 58.3874 | 14.3541 | 79.3858 |
| 3 | 172952 | 559839432 | 13 | 110.2600 | -69.1510 | 68.83630 | -51.3524 | 97.5720 | -0.504613 | 2.358470 | -1 | 13 | 88.3199 | 85.94400 | -16.81970 | -11.4510 | 87.5743 | -0.130388 | -0.193263 | -1 | -13 | 45.0987 | -19.98280 | -29.14080 | -28.0247 | 35.33410 | -0.727298 | -2.17188 | 1 | -13 | 9.79377 | 3.02072 | 8.34856 | -4.13324 | 8.87824 | -0.450186 | 1.223630 | 1 | 91.1877 | 37.3758 | 232.9290 |
| 4 | 167282 | 44166176 | -13 | 54.3881 | -27.4999 | -43.86520 | -16.6628 | 51.7726 | -0.316533 | -2.130770 | 1 | 13 | 39.8417 | 31.53530 | 18.85330 | 15.4088 | 36.7413 | 0.407975 | 0.538835 | -1 | -13 | 20.3208 | 3.30081 | 16.01250 | 12.0677 | 16.34910 | 0.683619 | 1.36750 | 1 | 13 | 6.83735 | 4.64276 | -2.38618 | 4.41465 | 5.22007 | 0.767963 | -0.474752 | -1 | 90.7513 | 14.7350 | 119.2900 |
Huomaamme selvästi, että 125 GeVin kieppeillä tapahtuu jotain oletustemme lisäksi. Tuloksemme ovat melko samansuuntaisia kuin varsinaiset CMS:n analyysitkin, erojen noustessa pääasiassa käyttämiemme menetelmien karkeudesta.


