Funktion sovittaminen histogrammiin

Tutustutaan tässä harjoituksessa siihen, miten histogrammiin voidaan tehdä sovite. Sovite on erinomainen työkalu, kun halutaan selvittää esimerkiksi jakauman odotusarvo ja hajonta. Hiukkasfysiikan tapauksessa tämä tulee kyseeseen, kun pyritään selvittämään histogrammissa olevan piikin paikkaa ja leveyttä.

Tutkitaan hiukkasfysiikan dataa sellaisista törmäyksistä, joissa on havaittu kaksi myonia. Data on haettu CERN:n avoin data portaalista ja se löytyy tämän notebookin kanssa samasta hakemistosta nimellä “Dimuon_DoubleMu.csv”.

Datan hakeminen ja piirtäminen

import pandas as pd
import matplotlib.pyplot as plt

data = pd.read_csv('Dimuon_DoubleMu.csv')
data.head()

	Run	Event	type1	E1	px1	py1	pz1	pt1	eta1	phi1	...	type2	E2	px2	py2	pz2	pt2	eta2	phi2	Q2	M
0	165617	74601703	G	9.6987	-9.5104	0.3662	1.8633	9.5175	0.1945	3.1031	...	G	9.7633	7.3277	-1.1524	6.3473	7.4178	0.7756	-0.1560	1	17.4922
1	165617	75100943	G	6.2039	-4.2666	0.4565	-4.4793	4.2910	-0.9121	3.0350	...	G	9.6690	7.2740	-2.8211	-5.7104	7.8019	-0.6786	-0.3700	1	11.5534
2	165617	75587682	G	19.2892	-4.2121	-0.6516	18.8121	4.2622	2.1905	-2.9881	...	G	9.8244	4.3439	-0.4735	8.7985	4.3697	1.4497	-0.1086	1	9.1636
3	165617	75660978	G	7.0427	-6.3268	-0.2685	3.0802	6.3325	0.4690	-3.0992	...	G	5.5857	4.4748	0.8489	-3.2319	4.5546	-0.6605	0.1875	1	12.4774
4	165617	75947690	G	7.2751	0.1030	-5.5331	-4.7212	5.5340	-0.7736	-1.5522	...	G	7.3181	-0.3988	6.9408	2.2825	6.9523	0.3227	1.6282	1	14.3159

5 rows × 21 columns

plt.hist(data['M'], bins=300)
plt.show()

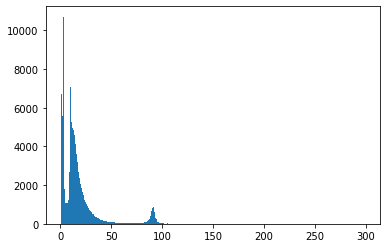
Rajataan tarkastelumme invariantin massan välille 80 GeV - 100 GeV ja piirretään data tällä välillä. Huom. Tällä kertaa plt.hist()-funktion paluuarvot on otettu talteen. Funktiolla on kolme paluuarvoa, joista meitä kiinnostaa kaksi ensimmäistä: histogrammin pylväiden arvot sekä pylväiden reunat.

alaraja = 80
yläraja = 100
pylväitä = 100

plt.figure()
arvot, reunat, _ = plt.hist(data['M'], bins=pylväitä, range=(alaraja, yläraja))
plt.xlabel('Invariantti massa (GeV)')
plt.ylabel('Tapahtumien lukumäärä')
plt.show()

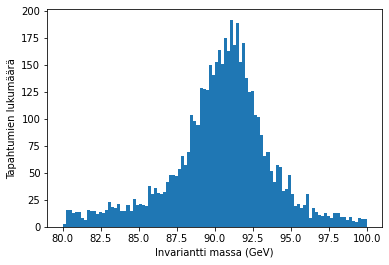
Sovitefunktion määritteleminen

Tavoitteenamme on tehdä sovite yllä olevaan jakaumaan. Hiukkasfysiikassa yleisesti käytettävä jakaumafunktio on Breit-Wigner -jakauma, mutta käytetään tässä Gaussin jakaumaa, joka ottaa taustatapahtumat myös huomioon.

Tällainen Gaussin funktio on muotoa:

\(f(x) = a\frac{e^{-(x-\mu)^2}}{2\sigma^2} + bx + c\),

missä \(a\) on kerroin, \(\mu\) odotusarvo, \(\sigma^2\) varianssi ja \(b\) ja \(c\) taustatapahtumiin liittyviä kertoimia.

Määritellään funktio:

import numpy as np

def gauss(x, *p):
    a, mu, sigma, b, c = p
    return a*np.exp(-(x-mu)**2/(2.*sigma**2)) + b*x + c

Sovitteen tekeminen

Tehdään seuraavaksi sovite scipy-paketin curve_fit -funktiolla. Meidän tulee kuitenkin ensin määrittää pylväiden keskikohdat, jotta sovite osuu oikealle kohdalle.

from scipy.optimize import curve_fit

# Pylväiden keskikohdat saadaan ottamalla kahden vierekkäisen reunan keskiarvo
keskikohdat = (reunat[:-1] + reunat[1:])/2

# Sovitetta varten tarvitaan sopivat alkuarvaukset. Jos sovite epäonnistuu, kokeile jotain muita alkuarvoja
# Alkuarvot ovat järjestyksessä a, mu, sigma, b, c
p0 = [100, 90, 1, 1, 1]

# Lasketaan optimaaliset kertoimet
kertoimet, _ = curve_fit(gauss, keskikohdat, arvot, p0=p0)

# Lasketaan sovite kertoimien avulla
sovite = gauss(keskikohdat, *kertoimet)

# Piirretään alkuperäinen histogrammi sekä sovitefunktio
plt.hist(data['M'], bins=pylväitä, range=(alaraja, yläraja))
plt.plot(keskikohdat, sovite, label='Sovite')
plt.xlabel('Invariantti massa (GeV)')
plt.ylabel('Tapahtumien lukumäärä')

# Tulostetaan odotusarvo ja piikin leveys (FWHM)
print('Odotusarvo = ', kertoimet[1])
print('Piikin leveys = ', 2*np.sqrt(2*np.log(2))*kertoimet[2])

plt.show()

Odotusarvo =  90.8583262565214
Piikin leveys =  4.493052850735739

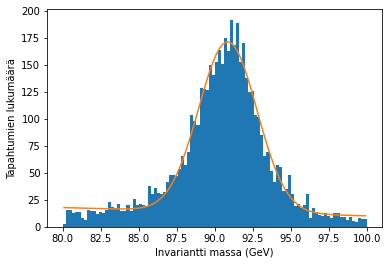
Tämän tuloksen perusteella saamme Z-bosonin massaksi noin 90,86 GeV. Kokeile, saatko sovitettua Breit-Wigner -jakauman histogrammiin. Onko sovite parempi kuin Gaussin jakauma? Kokeile myös, miten pylväiden lukumäärän muuttaminen vaikuttaa tulokseen.